Egy szavakat számolgató nyelvész felfedezett egyszer egy különleges statisztikai-eloszlást. A szavak eloszlásához hasonló mintázatokat láthatunk azonban az üzleti életben, a szoftverfejlesztésben, a városok lélekszámát vizsgálva is. Maradjon velünk az olvasó, a matematika helyett grafikonokkal eredünk a különös jelenség nyomába!
Pareto és a 80/20 szabály
A Pareto-elvet, vagy más néven 80/20 szabályt sokan ismerik, íme néhány példa rá a vonatkozó Wikipedia szócikkből:
- A profit 80%-a az ügyfelek 20%-tól származik.
- A reklamációk 80%-a az ügyfelek 20%-tól érkezik.
- A profit 80%-a a munkára fordított idő 20%-ból keletkezik.
- Az eladások 80%-a a termékportfólió 20%-ból keletkezik.
- Az eladások 80%-át a sales csapat 20%-a hozza.
A felsoroláshoz hozzátehetjük még a szoftverfejlesztésben használatos 80/20 elveket is:
- A hibák 80%-a a kód 20%-ában rejlik.
- A követelmények 20%-a adja a funkcionalitás 80%-át.

Tehát általában elmondhatjuk, hogy az esetek 20%-a eredményezi az okozatok 80%-át. Ezt az elvet általánosan Vilfredo Pareto fogalmazta meg először és matematikai szabatossággal kidolgozott hatványtörvényét ma Pareto-eloszlásnak hívjuk.
Long tail - sok kicsi, sokra megy
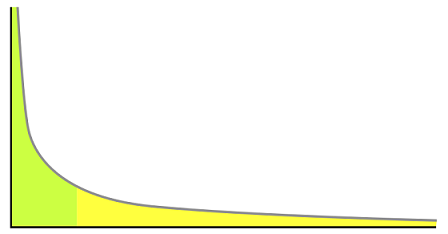
A legismertebb 80/20 szabály a long tail vagy hosszú farok, melyet Chris Anderson azonos című (magyarul is olvasható) könyve vezetett be a köztudatba. A fenti görbét megfigyelve láthatjuk, hogy az első 20% alatti terület kb. megegyezik a maradék 80% alattival. Anderson szerint a modern technológiák lehetővé teszik, hogy a kis mennyiségben árusított termékek is elérjenek a potenciális vásárlókhoz, ami kb. ugyanakkora piacot jelent, mint a nagy volumenben értékesített, könnyen eladható áruké.
Normál eloszlás
Ha egy mintázatot sokszor megfigyelhetünk a világban, akkor az segíthet minket szisztematikus összefüggések feltárásában. Az egyik legismertebb mintázat az ún. normál eloszlás. A statisztikai adatgyűjtés kezdetétől fogva megfigyelték, hogy az emberek magassága, testsúlya, halálozása stb. nagyjából egyforma képet mutat. Az alábbi ábrán 10.000 ember magasságát ábrázoljuk (amerikai adatokat használtunk a Machine Learning for Hackers c. könyvhöz kapcsolódó kódtárból, az értékek inchben vannak).
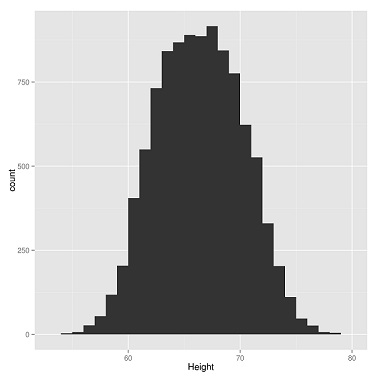 Látható, hogy a legtöbben 65-70 inch (165-178 cm) közötti tartományba tartoznak és az ettől magasabb vagy alacsonyabb (jobbra és balra) emberek száma fokozatosan csökken a szélső értékek felé közelítve. Ha szétválasztjuk a férfiakat és a nőket, akkor sokkal szimmetrikusabb grafikonokat kapunk.
Látható, hogy a legtöbben 65-70 inch (165-178 cm) közötti tartományba tartoznak és az ettől magasabb vagy alacsonyabb (jobbra és balra) emberek száma fokozatosan csökken a szélső értékek felé közelítve. Ha szétválasztjuk a férfiakat és a nőket, akkor sokkal szimmetrikusabb grafikonokat kapunk.
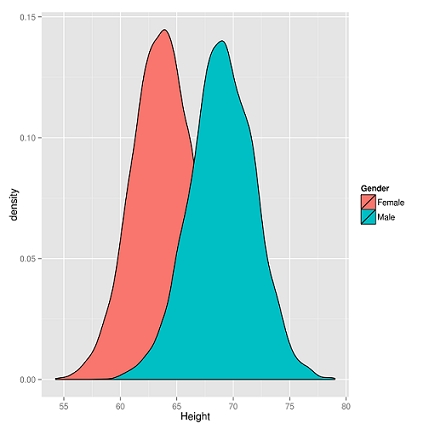
A fenti ábrát összevetve láthatjuk, hogy mind a férfiak, mind a nők magassága majdnem tökéletesen haranggörbe alakú.
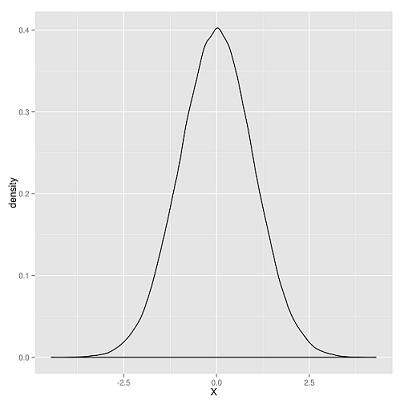
A fenti ábrán egy "hipotetikus" normál eloszlás látható. A statisztikában ez nagyon hasznos, mivel ezzel a hipotetikus és ideális normál eloszlással viszonylag könnyű számolni, sokat tudunk róla és megbízhatóan működik. Tapasztalat alapján arra jutottak a statisztikusok, hogy a legtöbb jelenség követi a normál eloszlást (azaz közelíti, különösen ha sok megfigyelést tudunk végezni) aminek örülünk, mert nagyon kényelmes ilyen eloszlású adatokkal dolgozni.
Zipf törvénye
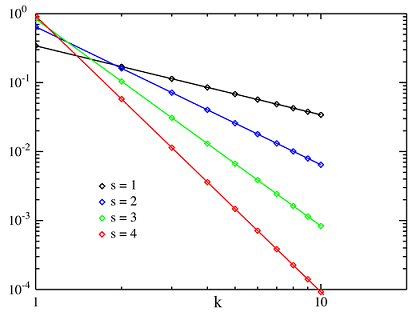
Pareto-elve, a hosszú farok és a sok megfigyelés támasztja alá, hogy a 80/20 szabály mögött valami általánosabb rejlik. Ezt először George Kingsley Zipf fedezte fel szógyakorisági vizsgálatai során. A róla elnevezett törvény kimondja, hogy egy szó gyakorisága fordítottan arányos a frekvenciatáblában (csökkenő sorrendű szógyakorisági táblázat) szereplő sorszámával. A következő ábrán látható pár ideális Zipf-eloszlás.
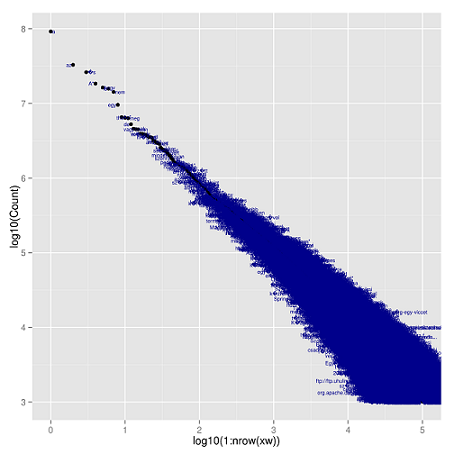
A Magyar Webkorpusz 10.000 leggyakoribb elemét mutatja az alábbi grafikon (a vízszintes tengelyen a frekvenciatáblában elfoglalt pozíciót, a függőlegesen pedig a gyakorisági értéket mutatjuk). Láthatjuk, nem tökéletesen követi a hipotetikus Zipf-eloszlást, de azért hasonlít rá.
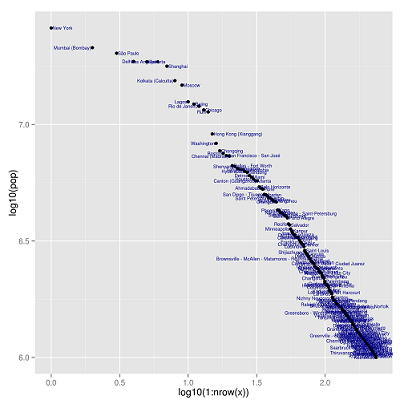
Zipf törvénye világvárosokra alkalmazva
A szógyakoriság mellett Zipf törvényét előszeretettel alkalmazzák a társadalomtudományokban is, erről a területről a legtöbben a városok lélekszáma és a lakosság szerinti sorrendben elfoglalt pozíció közötti fordított arányosságot ismerik. Az alábbi ábra a nagyobb világvárosok Zipf-eloszlását szemlélteti. (A PopulationData.net oldal adatait használtuk a grafikonok elkészítéséhez.)
Érdekes, hogy országokon belül is láthatjuk ezt az eloszlást (ha nem is olyan tökéletesen).
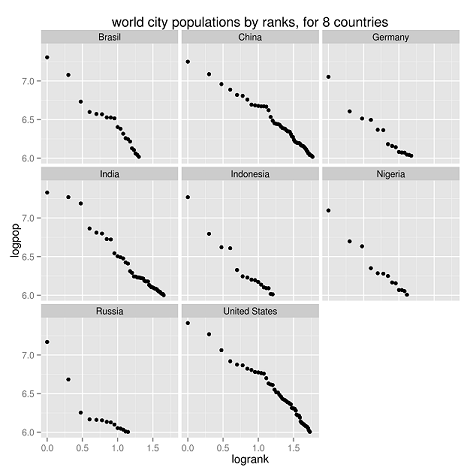
A fenti nyolc ország adatait összesítve az alábbi grafikont kapjuk.
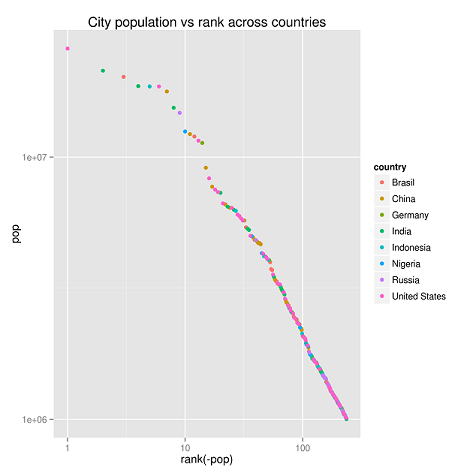
Egy grafikonon szemléltetve jobban látszik, hogy országokon belül is megismétlődik a Zipf-eloszlás.
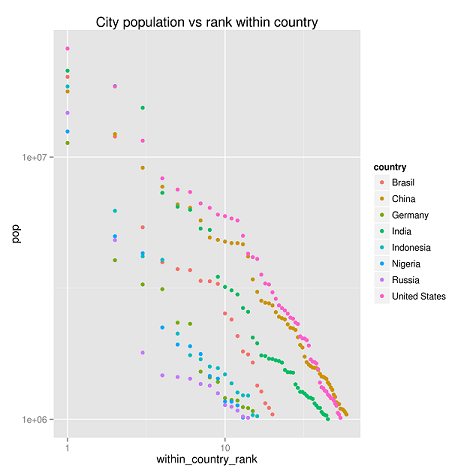
Zipf törvénye a magyar települések esetében is működik
Az alábbi ábrát a KSH Magyaroszág közigazgatási helynévkönyve 2012. január 1. táblája alapján készítettük.
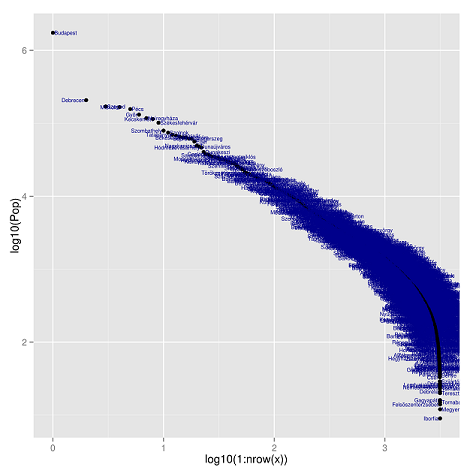
A fenti ábrán látható, hazánk sem kivétel a globális trendek alól. Az összes magyar települést vizsgálva látható, hogy Budapest kilóg a sorból és a vízszintes tengely végéhez közeledve nagyon sok apró település eltéríti a görbét az "ideális iránytól".
Hol használható Zipf-törvénye
A Zipf-törvény a keresésben és információkinyerésben arra a felismerésre vezetett, hogy a leggyakoribb szavak túl sok zajt okoznak. Az ún. funkciószavakat (névelők, kötőszók stb.) általában stoplistába gyűjtve kiszűrik a feldolgozás során. Előszeretettel alkalmazzák az ún. inverz frekvenciatáblákat, mivel az alacsony gyakoriságú szavak különböztetik meg általában az egyes dokumentumokat.
Az internetes áruházak életében a Zipf-törvény (és változatai) nagyon nagy szerepet játszanak. Egyrészt a készlettervezésben érvényesül a 80/20 szabály, de a kiszállításban is megjelenik a Zipf-eloszlás.
Az internetes biztonsági alkalmazások is előszeretettel vizsgálják a felhasználói logok hosszú farkát. Az ún. anomáliadetekció abból indul ki, hogy legtöbb felhasználó a 80/20 szabály szerint viselkedik és a logok 80%-a az ismétlődő viselkedési formák 20%-át tartalmazza (pl. böngészés, chatelés, e-mailezés stb.) a gyanús és potenciálisan veszélyes dolgok a log 20%-ban találhatóak (melyek viszont az észlelt tevékenységek 80%-át tartalmazzák).
Amikor Zipf becsap minket

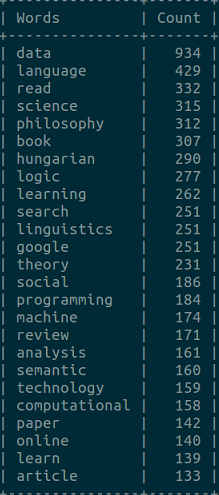
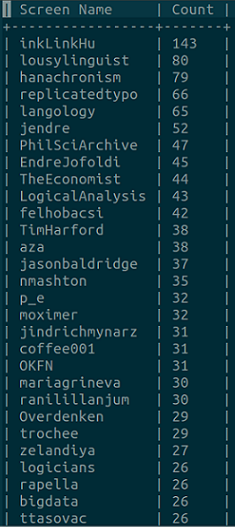
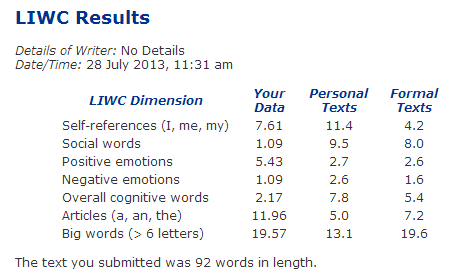
A nyelvtechnológiában egyre elterjedtebb emócióelemzésben és a törvényszéki nyelvészetben is egyre nagyobb figyelmet szentelnek a funkciószavaknak és a gyakorisági tábla első 20%-ába eső elemeknek. Habár egy beszélő számára lehetetlen észrevennie, hogy mely ismerőse használ több névelőt, egyre több kutató talál erős korrelációt pszichológiai faktorok és a funkciószavak gyakorisága között (l. Mit árul el rólad a Twitter fiókod és Nekünk elmélet kell című korábbi írásainkat). A szerzőség megállapításakor (legutóbb pl. J.K. Rowling esetében) is a gyakori szavak használati arányában meglévő apró különbségek vizsgálata kezd előtérbe kerülni.
Az anomáliadetekció területén is egyre nagyobb figyelmet szentelnek a megszokott viselkedés vizsgálatára. Ennek oka elsősorban az ún. nem szándékos károkozás megakadályozása volt (pl. amikor egy fájl helyett egy egész könyvtárat töröl valaki, vagy egyszerre több programot futtat, ami lassítja más, fontos programok működését stb.). Több teljesen normális esemény láncolata rossz dolgokhoz vezethet. Ilyen láncolatok kialakulhatnak véletlenül is, de akár szándékosan is.
Úgy tűnik a Zipf-eloszlás szorosan kapcsolódik az ember alkotta dolgokhoz, legyenek azok szavak, városok vagy e-kereskedelmi oldalak. Az elsőre pofonegyszerű összefüggés felbukkanhat mindenhol, nem árt számolni vele!






.jpg)