Az emberalkotta jelenségeket áthatják a hatványtörvények, melyekre először egy szavakat számolgató nyelvész figyelt fel, de a szógyakoriságon túl azóta a népesség eloszláson át a webes hálózatok topológiájáig sok mindenre alkalmaznak manapság. Politikai blogokról indított crawler-ünk eredményeinek értelmezése során sem mehetünk el ezek mellett.
A blogok világában nincs egyenlőség
Korábbi posztunkban már ismertetett crawler-ünk erről a seed listáról indult el. Az egyes doménekről begyűjtött egyedi url-ek száma az alábbiak szerint alakult:
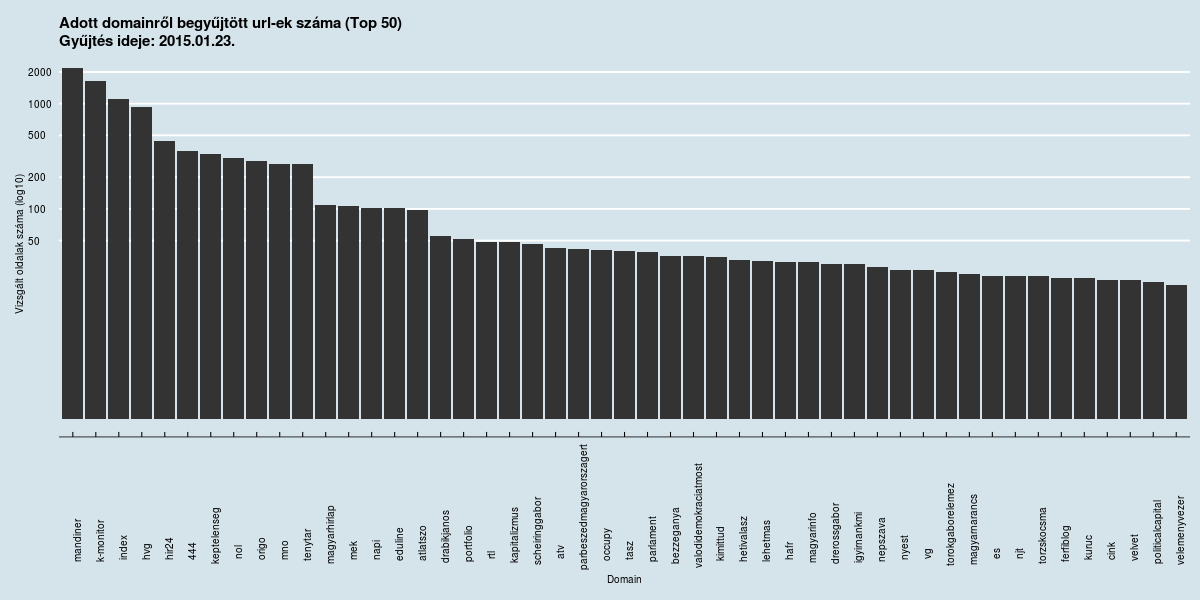
Láthatjuk, csupán az első három domén esetében került be több mint 1000 egyedi oldal, ezek közül csupán a Mandiner szerepelt a kiindulási pontok között. Ahogy haladunk a top ötvenes listán lefelé, láthatjuk, nagyságrendi különbségek vannak a helyezettek között. A negyedik és ötödik helyezettről már csak ötszáz és ezer közötti oldalt, a hatodik és tizenegyedik helyezett esetében már csak két-háromszáz, a tizenhatodik helyezésig már csak száz, a tizenhetediktől az ötvenedikig kb. ötven oldallal képviselteti magát egy domén a gyűjtésben.Ha tovább haladnánk, akkor még drámaibb esést láthatnánk, a következő ötven oldal már csak tíz, majd öt, végül kettő-három és a jelentős többség csak egy-egy egyedi url-lel került a korpuszba. Hogy lehetséges ez?
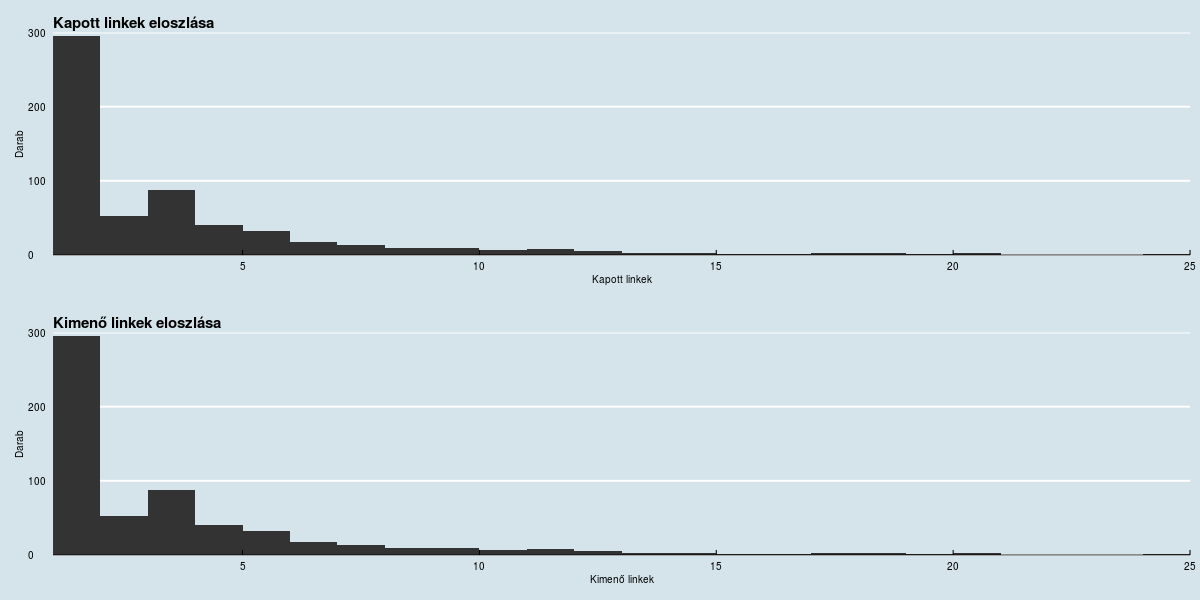
A fenti ábrán látható, az oldalak jelentős része egy linket kap csupán. Szinte ugyanezt a képet mutatja a kimenő linkek eloszlása is (már ha tartalmaz egyáltalán linket egy adott oldal, ne feledjük, mi csak a tartalomban lévő hivatkozásokat követtük!).
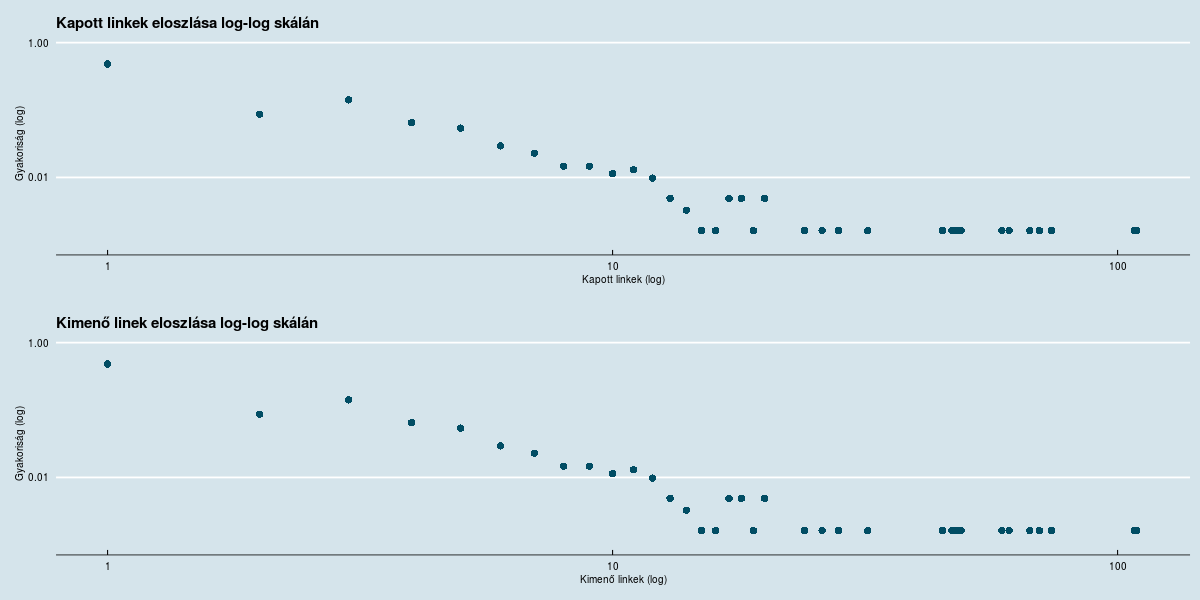
Log-log skálán ábrázolva a ki- és bemenő linkek eloszlása jobban szemlélteti, hogy a legtöbb oldal egy linket indít vagy kap, de akadnak olyan oldalak, melyekre az átlagosnál jóval többen linkelnek, illetve melyek szeretnek egy-egy írásban sokat linkelni (ez utóbbiak általában listák).
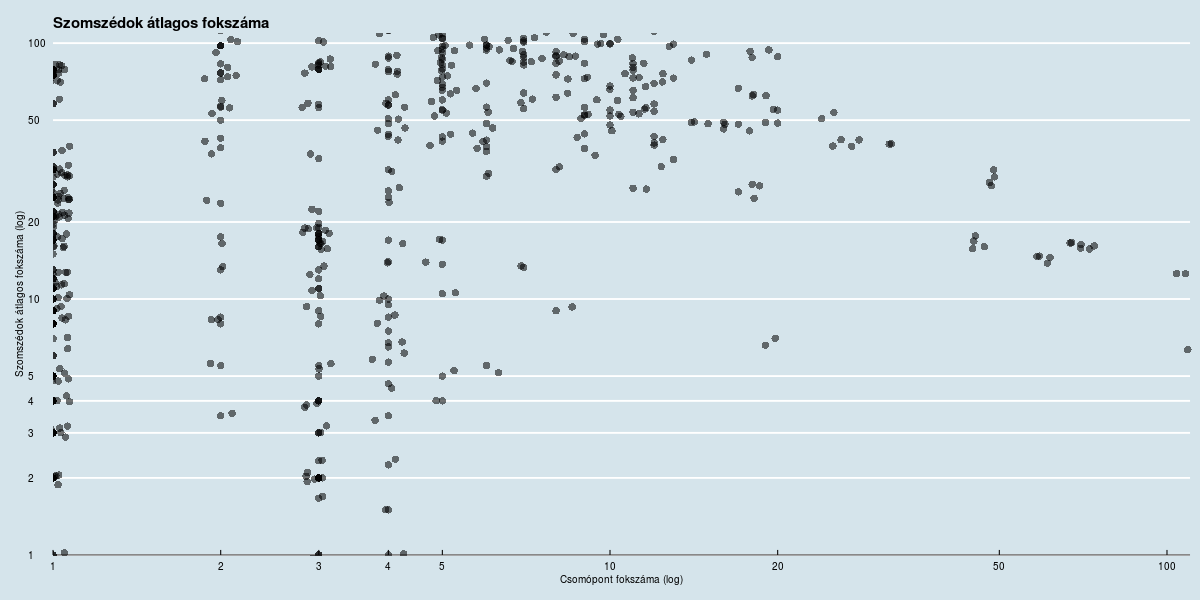
Ha megnézzük a fenti ábrán, hogy egy-egy oldalnak milyenek a szomszédai (azaz a melyekre linkel, vagy melyektől kap linket), akkor érdekes dologra figyelhetünk fel. Ahogy látható, a "kicsik" azaz az alacsony fokszámúak heterogén közegben vannak, szomszédaik között megtalálhatóak alacsony, közepes és magas fokszámú oldalak is. Láthatjuk azt is, hogy minél magasabb egy oldal fokszáma, annál válogatósabb szomszédai tekintetében. A fenti adatok azt támasztják alá, hogy az általunk vizsgált hálózat is ún. skálafüggetlen, s hatványfüggvényekkel (ezért a sok logartimus a plotokon) írható le. De mit is jelent ez?
Normális?????
A legtöbb dolog a valószínűleg jól ismert normális eloszlással írható le. Ilyen pl. a testmagasság. Ha sok férfi és nő magasságát megmérjük, akkor ilyesmi ábrát kapunk:
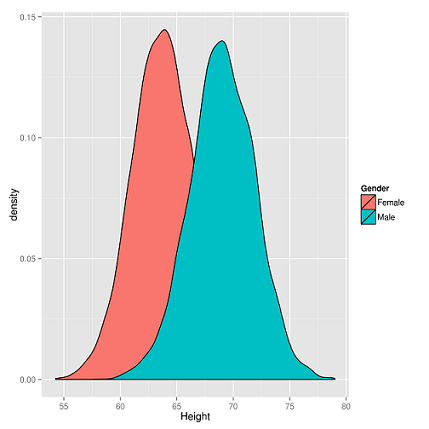
A statisztikában ez nagyon hasznos, mivel ezzel a hipotetikus és ideális normál eloszlással viszonylag könnyű számolni, sokat tudunk róla és megbízhatóan működik. Tapasztalat alapján arra jutottak a statisztikusok, hogy a legtöbb jelenség követi a normál eloszlást (azaz közelíti, különösen ha sok megfigyelést tudunk végezni) aminek örülünk, mert nagyon kényelmes ilyen eloszlású adatokkal dolgozni.
Szavak
Azonban valahogy az ember alkotta dolgok esetében nem mindig működik a normális eloszlás. George Kingsley Zipf fedezte fel szógyakorisági vizsgálatai során a róla elnevezett törvényt, mely kimondja, hogy egy szó gyakorisága fordítottan arányos a frekvenciatáblában (csökkenő sorrendű szógyakorisági táblázat) szereplő sorszámával. A következő ábrán látható pár ideális Zipf-eloszlás.
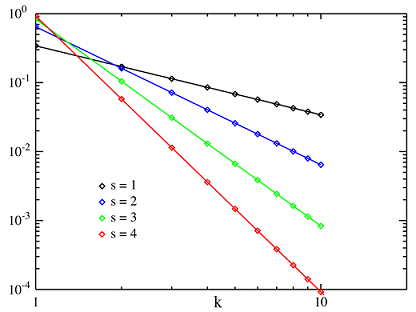
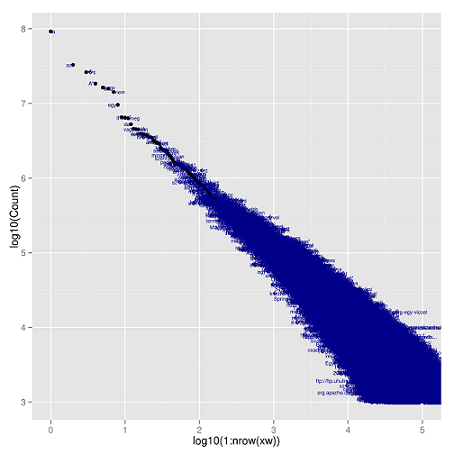
A Magyar Webkorpusz 10.000 leggyakoribb elemét mutatja az alábbi grafikon (a vízszintes tengelyen a frekvenciatáblában elfoglalt pozíciót, a függőlegesen pedig a gyakorisági értéket mutatjuk). Láthatjuk, nem tökéletesen követi a hipotetikus Zipf-eloszlást, de azért hasonlít rá.
Városok
A szógyakoriság mellett Zipf törvényét előszeretettel alkalmazzák a társadalomtudományokban is, erről a területről a legtöbben a városok lélekszáma és a lakosság szerinti sorrendben elfoglalt pozíció közötti fordított arányosságot ismerik.A PopulationData.net oldal adatait használva Brazília, Kína, Németország, India, Indonézia, Nigéria, Oroszország és az Egyesült államok nagyobb városainak összesített népesség szerinti listáját mutatjuk:
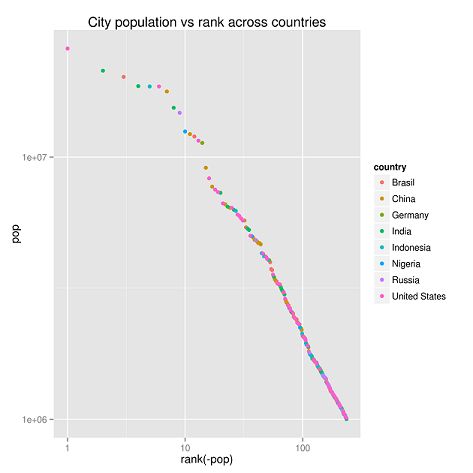
Az alábbi ábra mutatja, hogy a hatványeloszlás nem csak összesítve, hanem adott országokon belül is megjelenik.
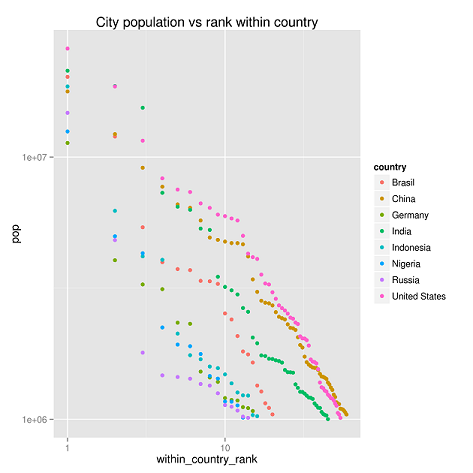
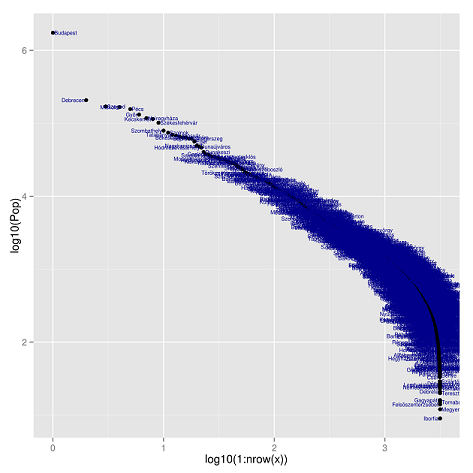
Az alábbi ábrát a KSH Magyaroszág közigazgatási helynévkönyve 2012. január 1. táblája alapján készítettük, reméljük látható, hazánk sem kivétel hatványtörvények alól.
80/20 szabály
A Zipf-eloszlást szokás diszkrét Pareto-eloszlásnak is nevezni. Vilfredo Pareto neve általában a 80/20 szabály kapcsán ismert, melyre néhány példa rá a vonatkozó Wikipedia szócikkből:
- A profit 80%-a az ügyfelek 20%-tól származik.
- A reklamációk 80%-a az ügyfelek 20%-tól érkezik.
- A profit 80%-a a munkára fordított idő 20%-ból keletkezik.
- Az eladások 80%-a a termékportfólió 20%-ból keletkezik.
- Az eladások 80%-át a sales csapat 20%-a hozza.
A felsoroláshoz hozzátehetjük még a szoftverfejlesztésben használatos 80/20 elveket is:
- A hibák 80%-a a kód 20%-ában rejlik.
- A követelmények 20%-a adja a funkcionalitás 80%-át.
A társadalmi egyenlőtlenségek terén is jelentkezik a Pareto-elv, mely szerint a javak 80%-ával a népesség 20%-a bír. A leghíresebb azonban az e-kereskedelemben bevett ún. hosszú farok, ami arra int minket, hogy a görbe elvékonyodó részén is van mit keresni. Az élet olyan, hogy a hatványeloszlást követi, a modern technika pedig elérhetővé teszi az elvékonyodó részt! Nem kell kétségbe esni ha nem kerülünk a top ötven oldal közé, vagy ha alacsony a PageRank értékünk, egy jó kereső segítségével és a keresőmarketing alkalmazásával megtalál minket az, aki kíváncsi ránk. Ahogy azokat a szavakat is használjuk a megfelelő helyen, melyek gyakorisága elenyésző, vagy ellátogatunk abba a városba is, ahol kevesen élnek.