Korábbi posztunkban a magyar Wikipedia korpuszán szemléltettük, hogy a nyelvi gráfok kisvilág tulajdonságot mutatnak. Most magyar példákon keresztül szemléltetjük, hogy a szemantikai és az asszociációs nyelvi hálózatok is skálafüggetlen kisvilágok.
Magyar WordNet
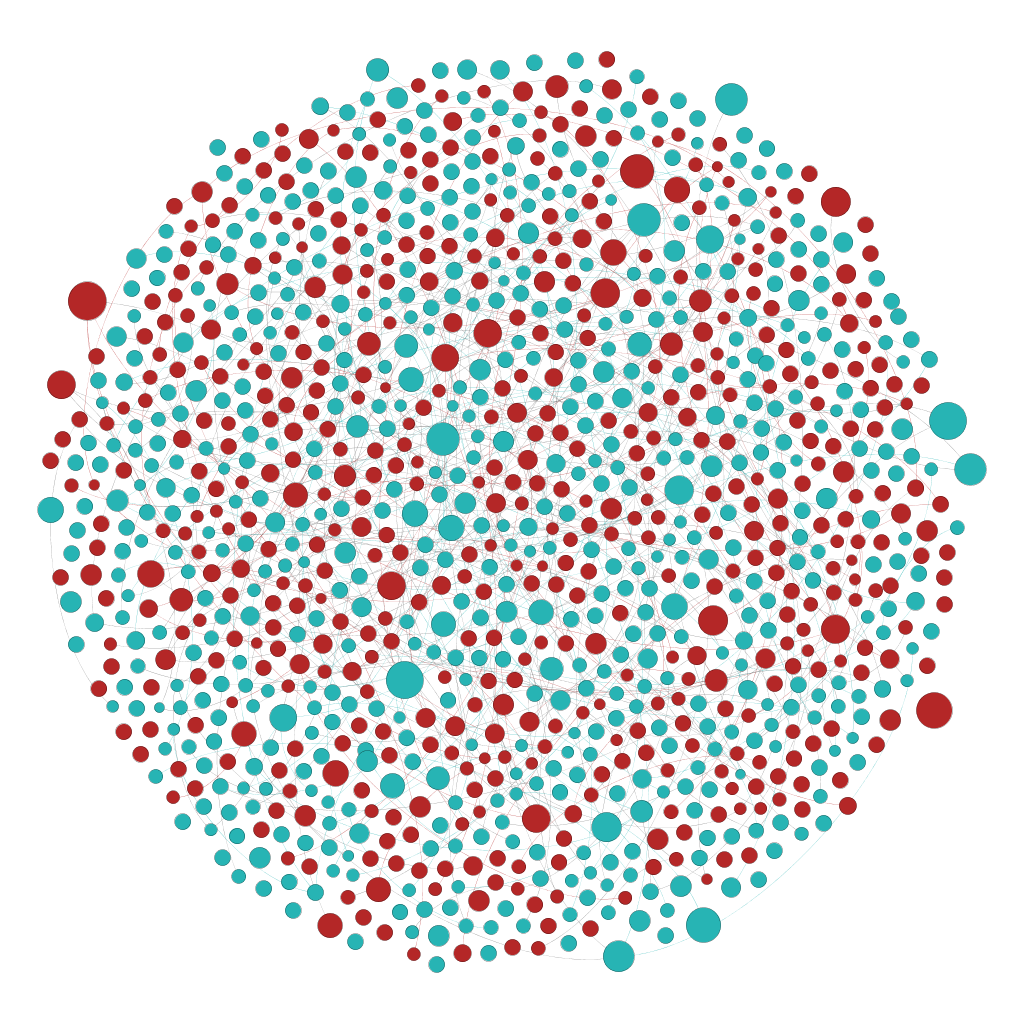
A Magyar WordNet az első magyar lexikális szemantikai adatbázis mely alapegységei az ún. synset-ek, melyekhez szinonimák, használati példák stb. tartoznak, továbbá az adott synset más elemekkel kapcsolatos szemantikai relációit sorolja fel. Hálózatunkat ebből készítettük, a fenti képen pirossal jelöltük a synset-eket, kékkel pedig a bennük felsorolt szinonimákat. Hálózatunkban 42359 csomópont található, ezek között 38335 él van. Az átlagos utak hossza 2.35, a gráf átmérője 13, klaszterezési együtthatója 0.0032. A fokszámok gyakorisága így alakul:
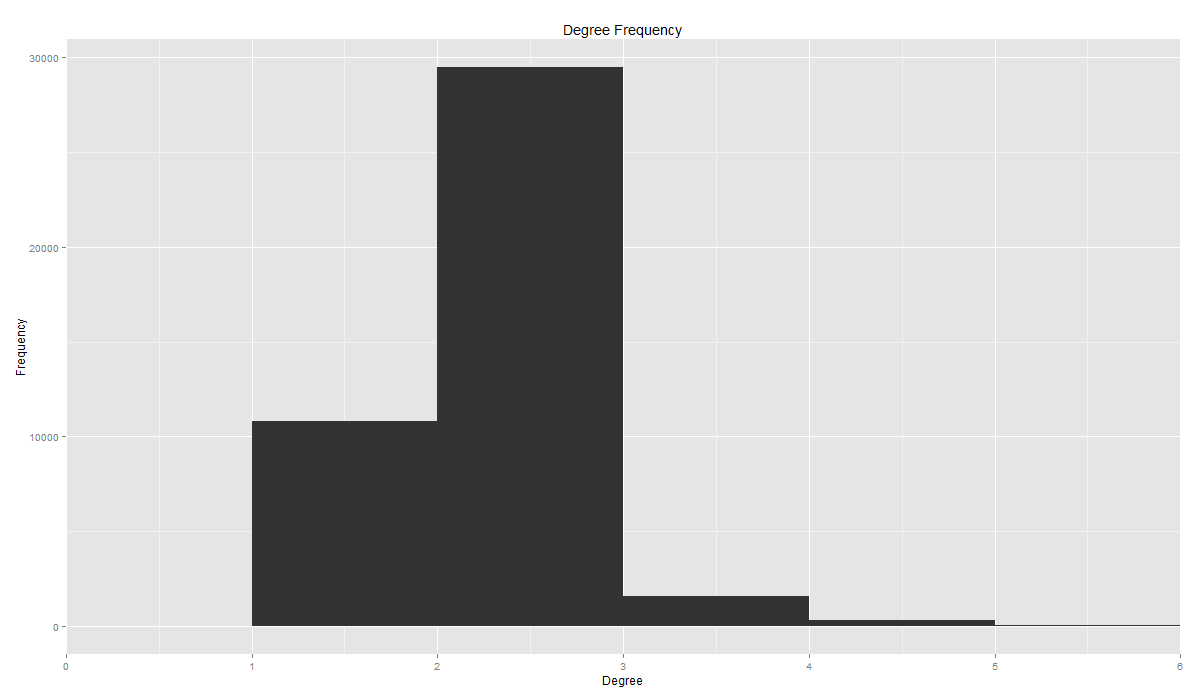
Ha a fokszámok eloszlását log-skálán nézzük, akkor a klasszikus skálafüggetlen gráfokra jellemző ábrát kapunk.
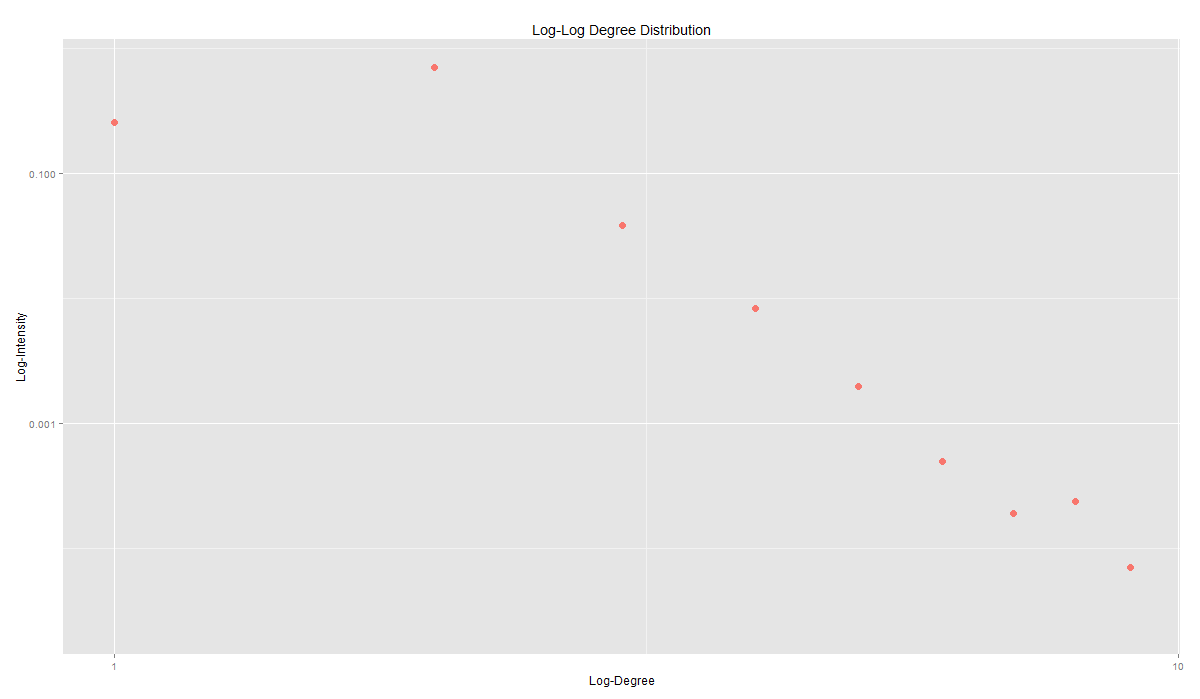
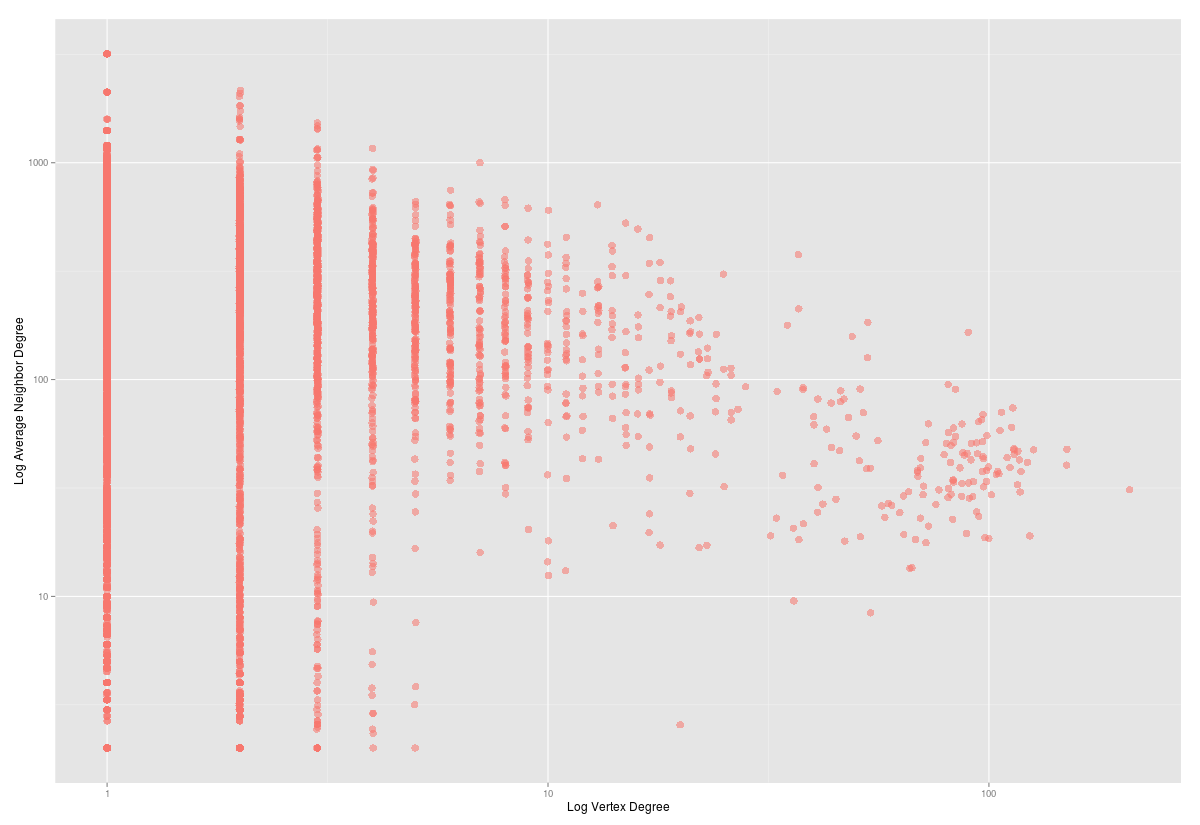
A WordNet esetében is érvényesül, hogy a népszerű csomópontok egyaránt vonzzák az alacsony és magas fokszámú elemeket, habár itt a klasszikus ábráktól kicsit eltérő képet láthatunk.
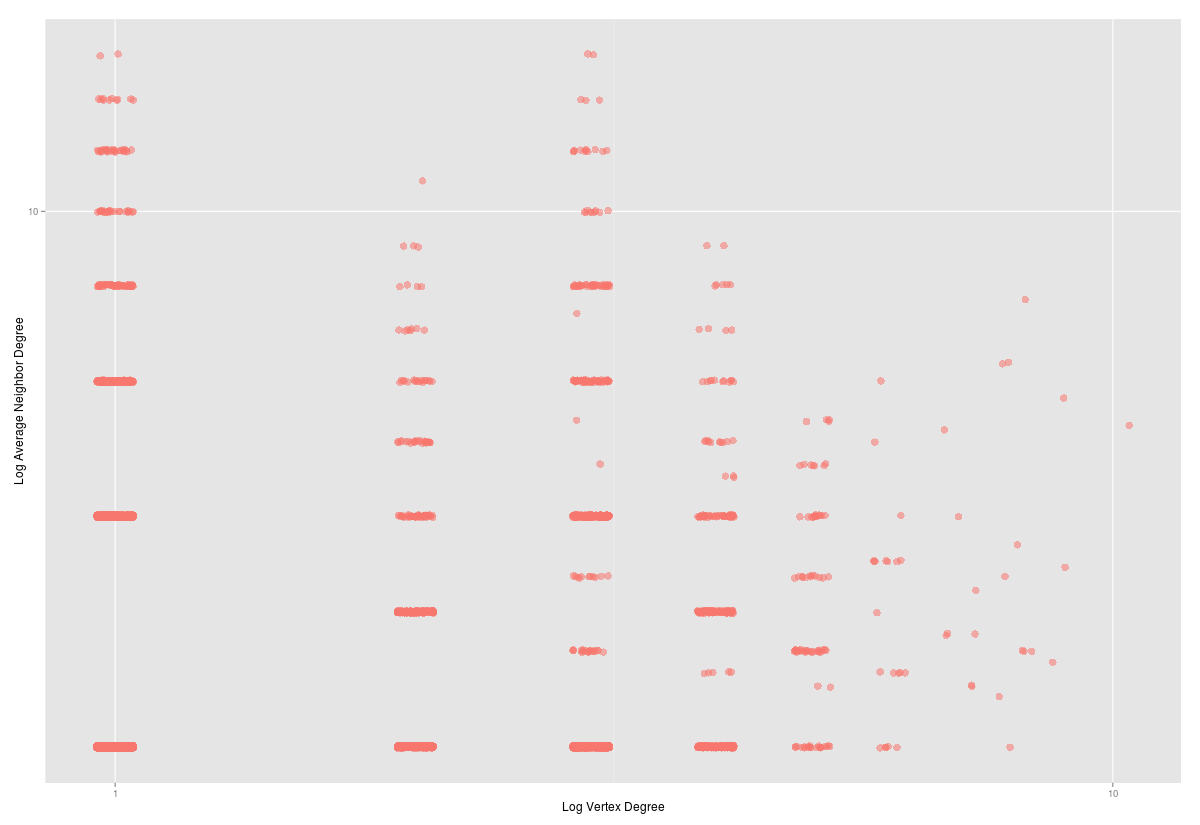
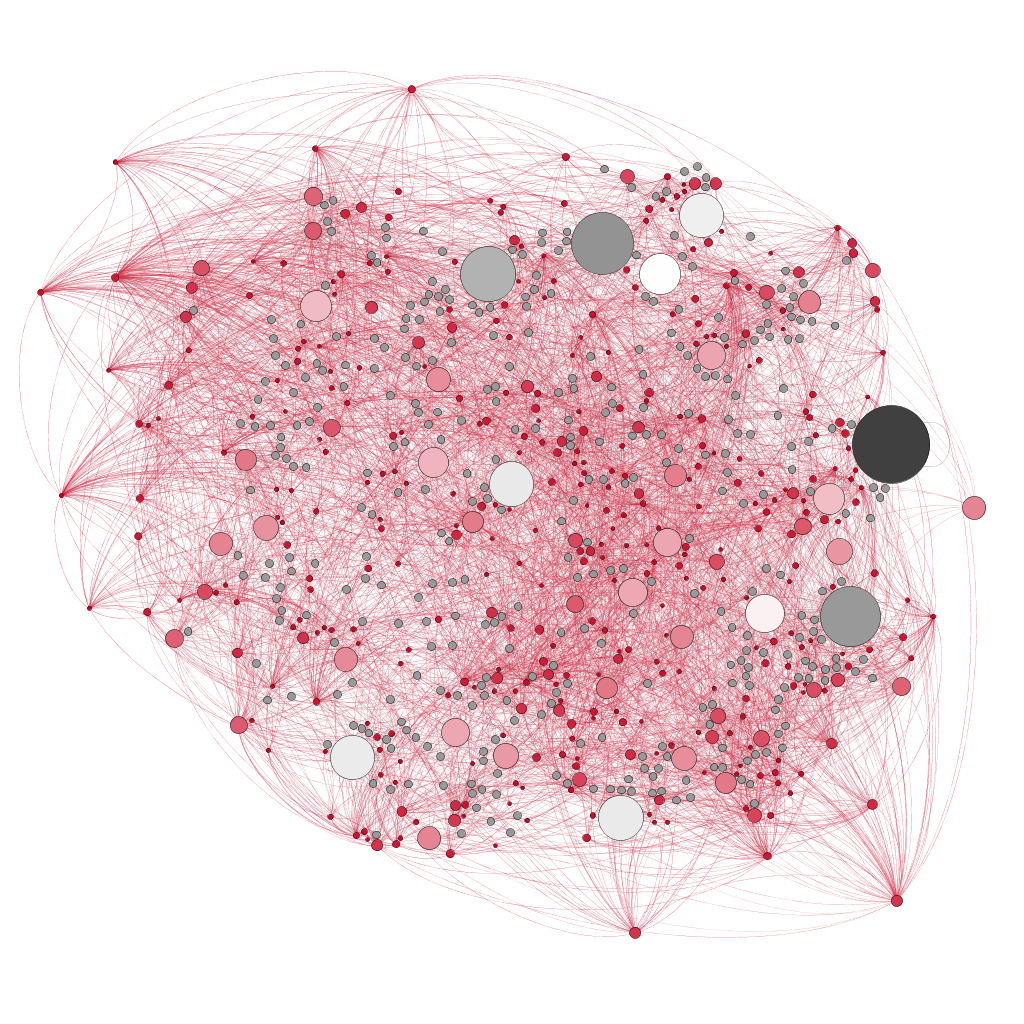
Mivel gráfunk nagy, úgy döntöttünk hogy a három vagy annál nagyobb fokszámú csomópontokat mutatjuk csak meg az alábbi ábrán. Továbbra is piros színnel jelöljük a synset-eket, kékkel pedig a szinonimákat. A csomópontok nagysága PageRank értéküket tükrözi. Érdemes megjegyezni, hogy a PageRank érték nem mutat akkora szórást mint más skálafüggetlen gráfok esetében.
Agykapocs
Kovács László Agykapocs adatbázisa egy online gyűjtött, többnyelvű szóasszociációs adatbázis. Sajnos az Agykapocs jelenleg nem érhető el online, de ebből a tanulmányból megismerhető. Akiknek ennyi nem elég, azoknak ajánljuk az adatbázis készítőjének doktori értekezéséből készült kötetet.
Mivel az Agykapocs többnyelvű, első körben leszűrtük a magyar kapcsolatokat. Irányított gráfunkba csak azok az elemek kerültek be, melyeket egynél több az erőssége, azaz egynél több felhasználó válaszaiban szerepelt. Az így kapott gráfban 8049 csomópont és 13635 él található. Az átlagos utak hossza 4.36, a gráf átmérője 353, klaszterezési együtthatója pedig 0.0438. A fokszám gyakoriságok alakulását az alábbi ábra szemlélteti:
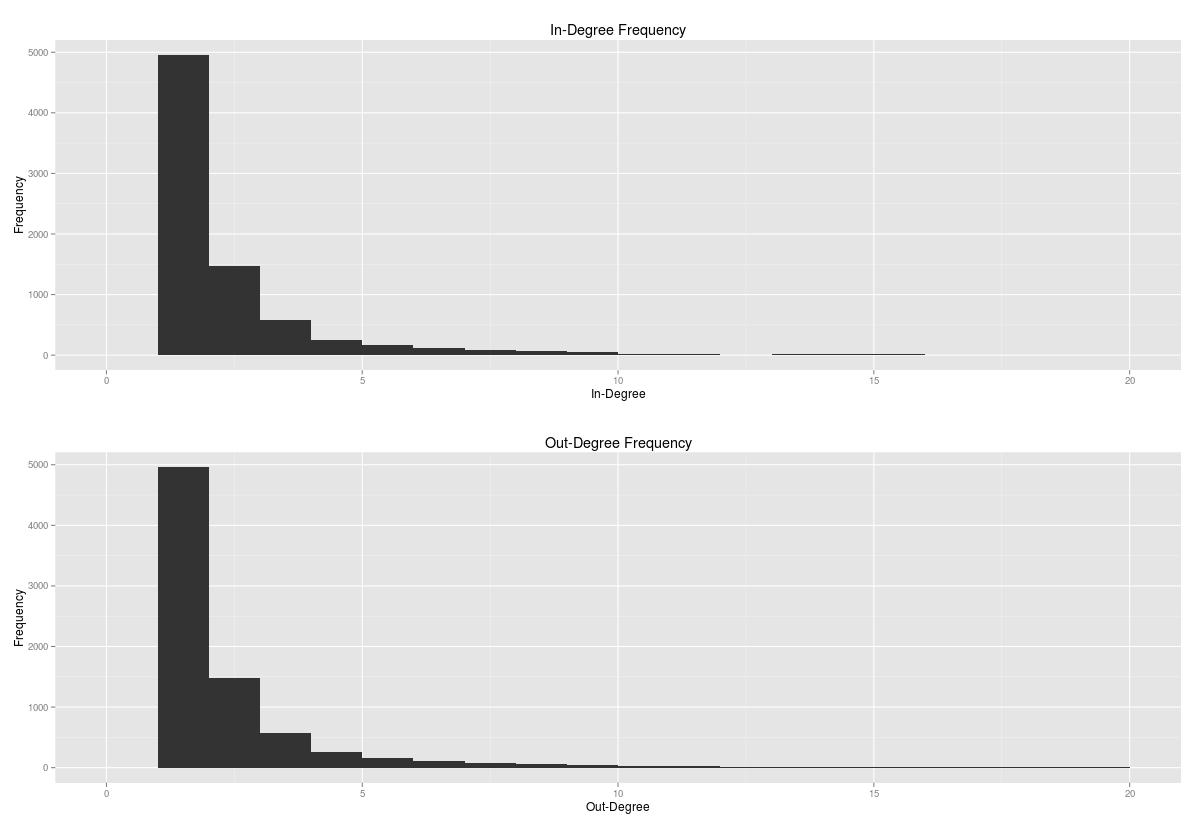
A fokszámok eloszlása is klasszikusan alakul.
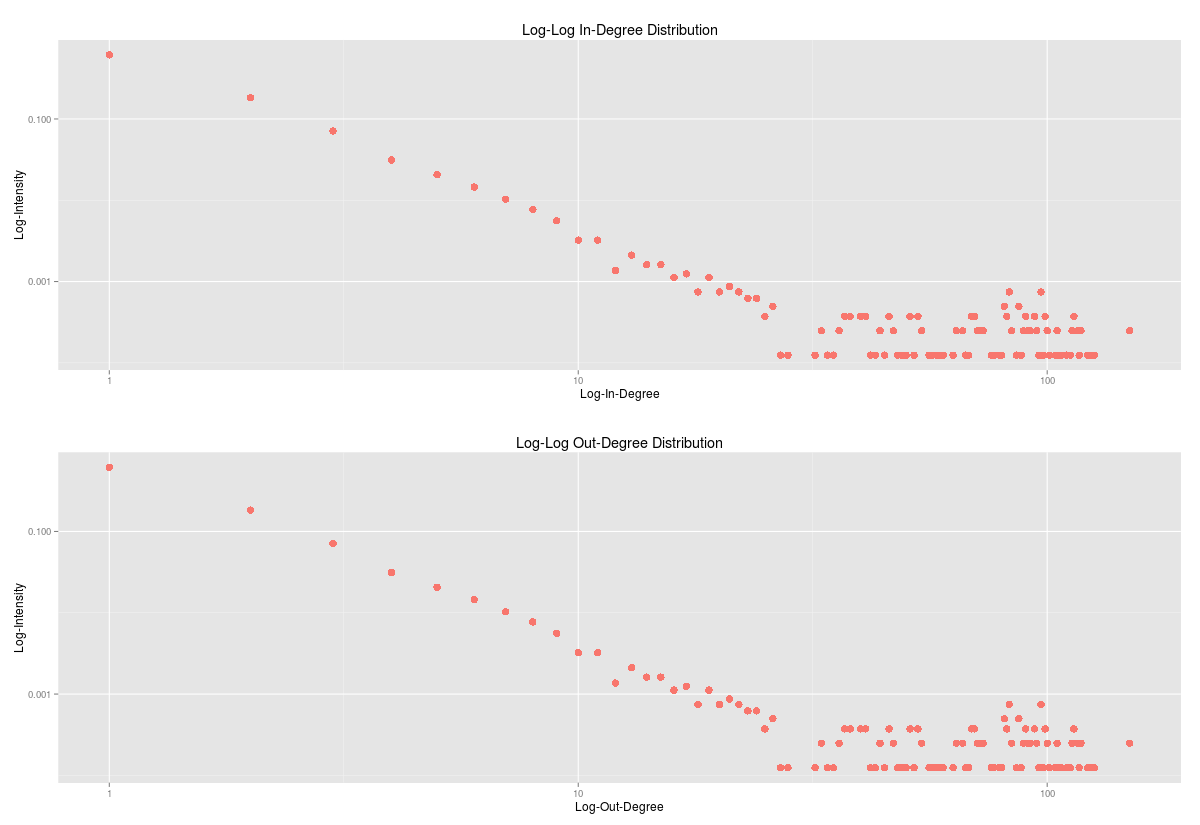
Nagyon szépen kijön a preferenciális kapcsolódás, azaz a népszerű csomópontokat mindenki szereti.
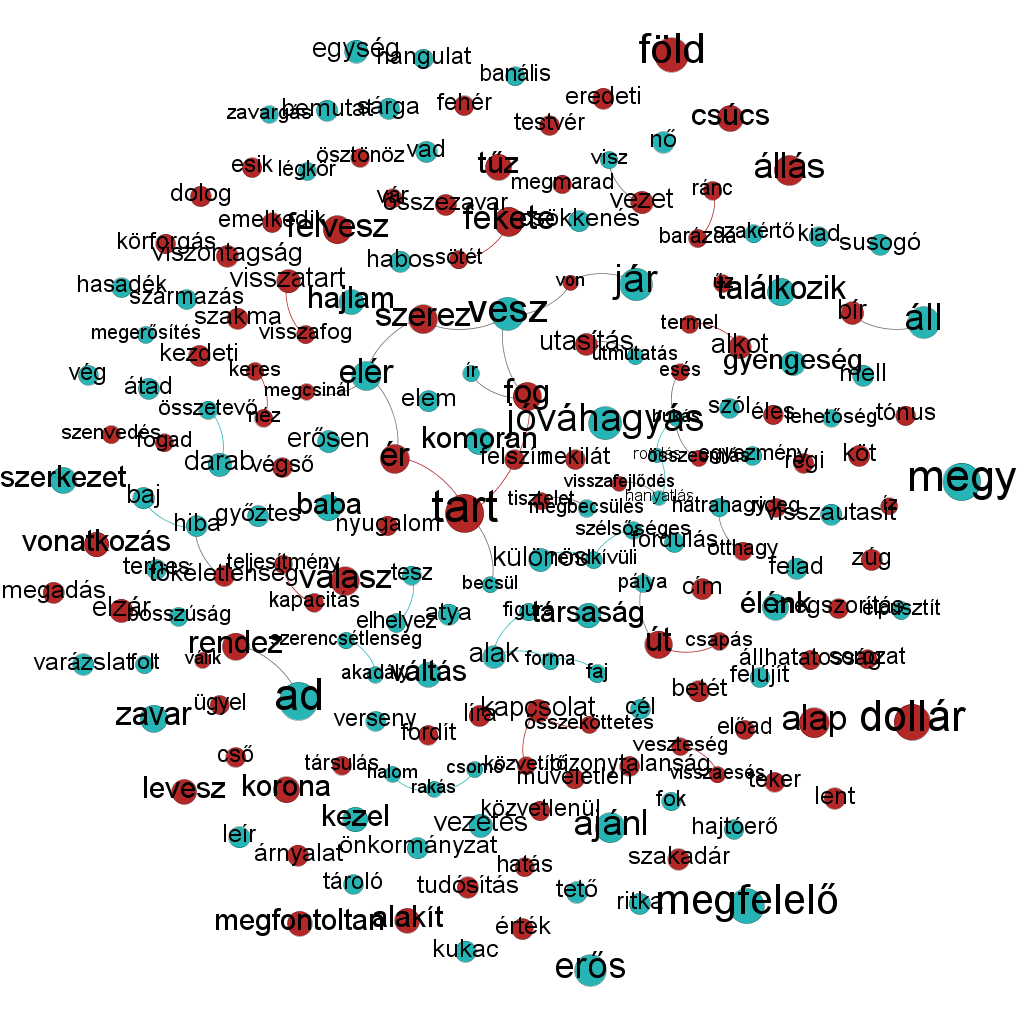
Az asszociációs hálózat megjelenítésével még nagyobb bajban voltunk, ugyanis ennek élei súlyozottak. Úgy döntöttünk, hogy a kilenc, vagy annál nagyobb fokszámú csomópontokat fogjuk megmutatni csupán.
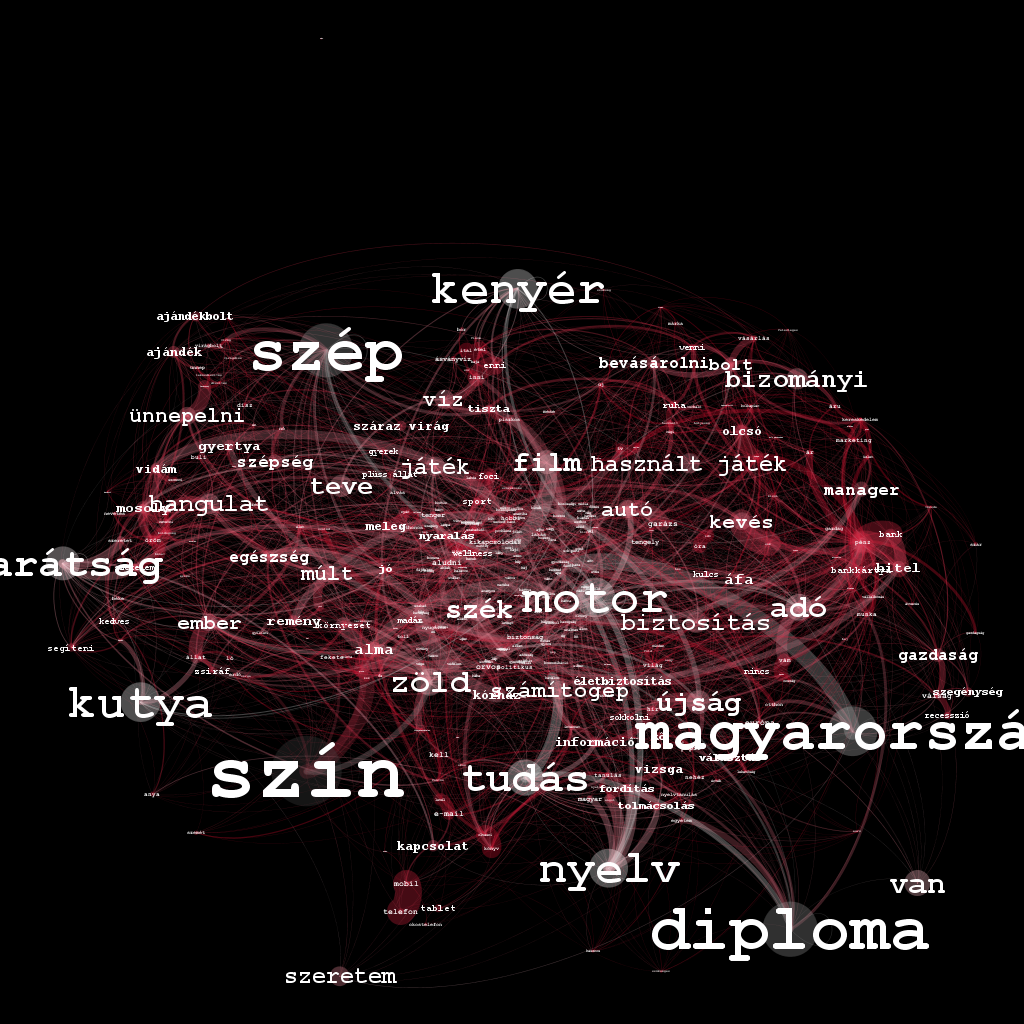
Szépnek szép, de mi értelme?
A nyelvi gráfok nagyon szexin mutatnak, de ennél sokkal többről van szó. Habár technológiai szempontból teljesen mindegy, hogy egy-egy nyelvtechnológiai megoldás hasonlít-e az emberi elmében lezajló folyamatokhoz, sok jel arra utal, hogy a gráf alapú megközelítés egyszerre hatékony mint technológiai eszköz és mint kognitív modell is. Hamarosan arról is írunk, miért gondoljuk ezt így!






