Watts és Storgatz kisvilág gráfjait már 2001-ben alkalmazta a(z angol) nyelvre Ferrer i Cancho és Solé. Sajnos azonban eredményük nem igazán ismert nyelvész körökben, pedig egyrészt túl tud mutatni a Zipf-féle hatványeloszláson, másrészt pedig alternatíváját nyújthatja a nyelvtechnológiában bevett hagyományos szózsák modellnek is, s talán a nyelvi rendellenességek magyarázatához is felhasználható. Nézzük meg magyar példán miről van szó!
Adatok
A magyar Wikipedia oldalai közül random kiválasztottunk párat, majd begyűjtöttük a szövegeket. 463409 szóból áll korpuszunk, ami 46096 egyedi szótári elem között oszlik el, ahogyan a hagyományosan Zipf nevéhez kötött grafikonunk is mutatja, a gyakoriság szerint első 10-100 szó bizony kiteszi a korpuszunk javát!
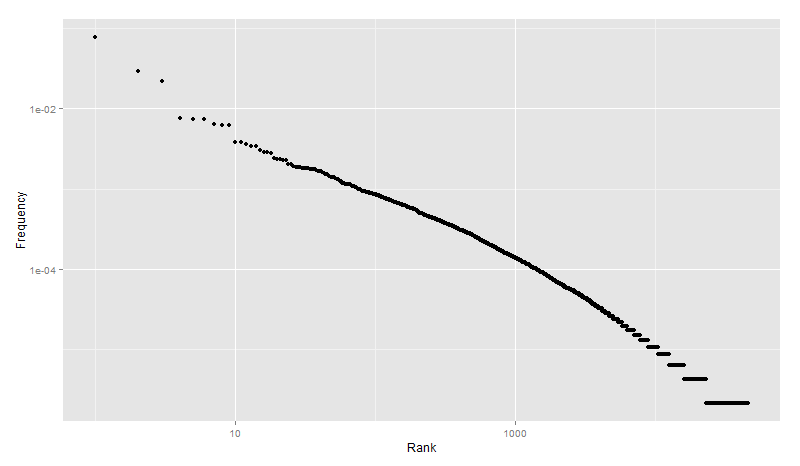
Tudjuk, a Zipf-eloszlás elején a funkciószavak és további, pár nagyon gyakori szó található. De hogy viszonyulnak ezek egymáshoz?
Hogy készítsünk kisvilág-gráfot szövegekből?
Mielőtt megvizsgálnánk gráfunkat, nézzük meg hogyan készült. Vegyük az alábbi gyógypéldát.
Zoli nagyon örül, mert Nóri elvitte végre krumplilángost enni. A krumplilángos Zoli számára a legfinomabb kaja a világon és reméli, hogy Nórinak is ízlett. Zoli és Nóri legközelebb nem krumplilángost fog enni, hanem elmennek megnézni az új Avengers filmet.
Ez szótövezve és minden nem-betűtől megtisztítva, csupa kisbetűsen így néz ki kb.:
zoli nagyon örül mert nóri vinni végre krumplilángos enni a krumplilángos zoli számára a finom kaja a világon és reméli hogy nóri is ízleni zoli és nóri közel nem krumplilángos fog enni hanem menni nézni az új avengers film
Ebből trigramokat készítünk.
zoli nagyon örül
nagyon örül mert
örül mert nóri
stb.
A gráfot a trigramokból készítjük. Két szó akkor kapcsolódik, ha együtt előfordul egy trigramban, a fenti példából az alábbi éleket kapjuk:
zoli - nagyon
zoli - örül
nagyon - örül
nagyon - mert
örül - mert
mert - nóri
stb.
Példánkból pedig az alábbi gráf generálható:
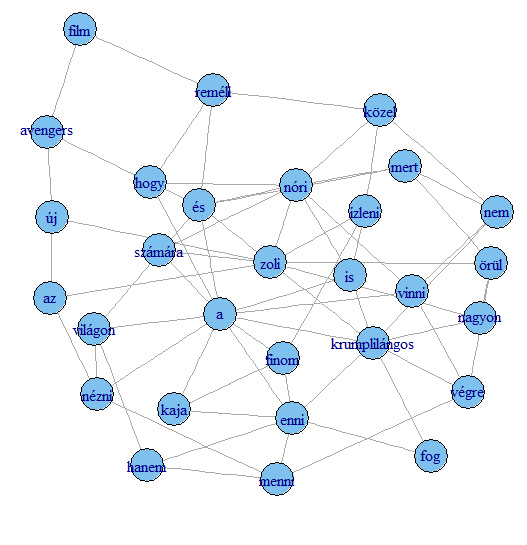
Pontosan így készült a mi gráfunk is, egy kis megkötéssel. A trigramok elemeiből csak akkor lettek csomópontok és közöttük élek, ha mindhárom tagjuk szerepelt a leggyakoribb 1500 szó listáján. Ezzel kicsit eltértünk a tanulmányban leírt módszertől, de nem lényegesen. (A tanulmány szerzői egyrészt gyakorisági küszöböt alkalmaztak, másrészt pedig az n-gramok tagjainak együttes előfordulásának valószínűségét is nézték)
Jellemzők
A fent leírt módon generált gráf 1500 csomópontot tartalmaz, melyek között 87749 él található. A fokszámeloszlást az alábbi ábra mutatja.
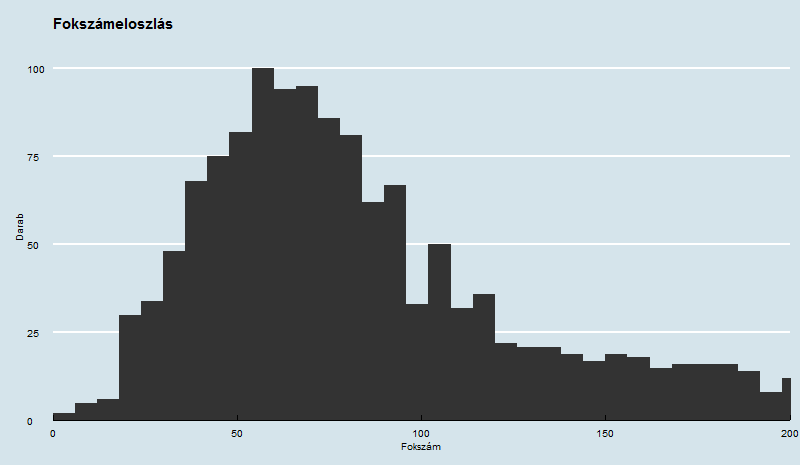
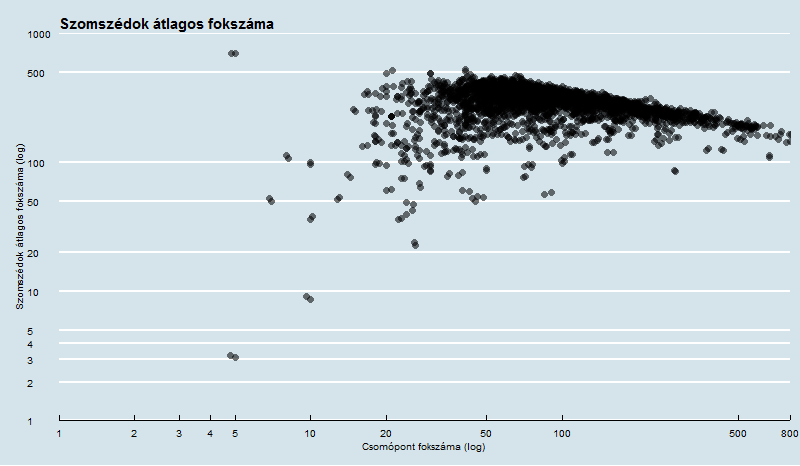
Jól látható, hogy egy kicsit eltérnek az adatok a klasszikus kisvilág-tulajdonságtól. Ennek oka, hogy a gráfban szerepel pár, a Wikipedia-ra jellemző szó (főleg a struktúra jelölésére használtak, ill. szerkesztéssel kapcsolatosak) melyeket nem szűrtünk ki. Ezek előfordulása gyakori, de általában ugyanolyan közegben fordulnak elő, ezért kevés szóhoz kapcsolódnak - emiatt vannak grafikonjaink "eltolva" a klasszikus kisvilágokat ábrázoló plotokhoz képest.
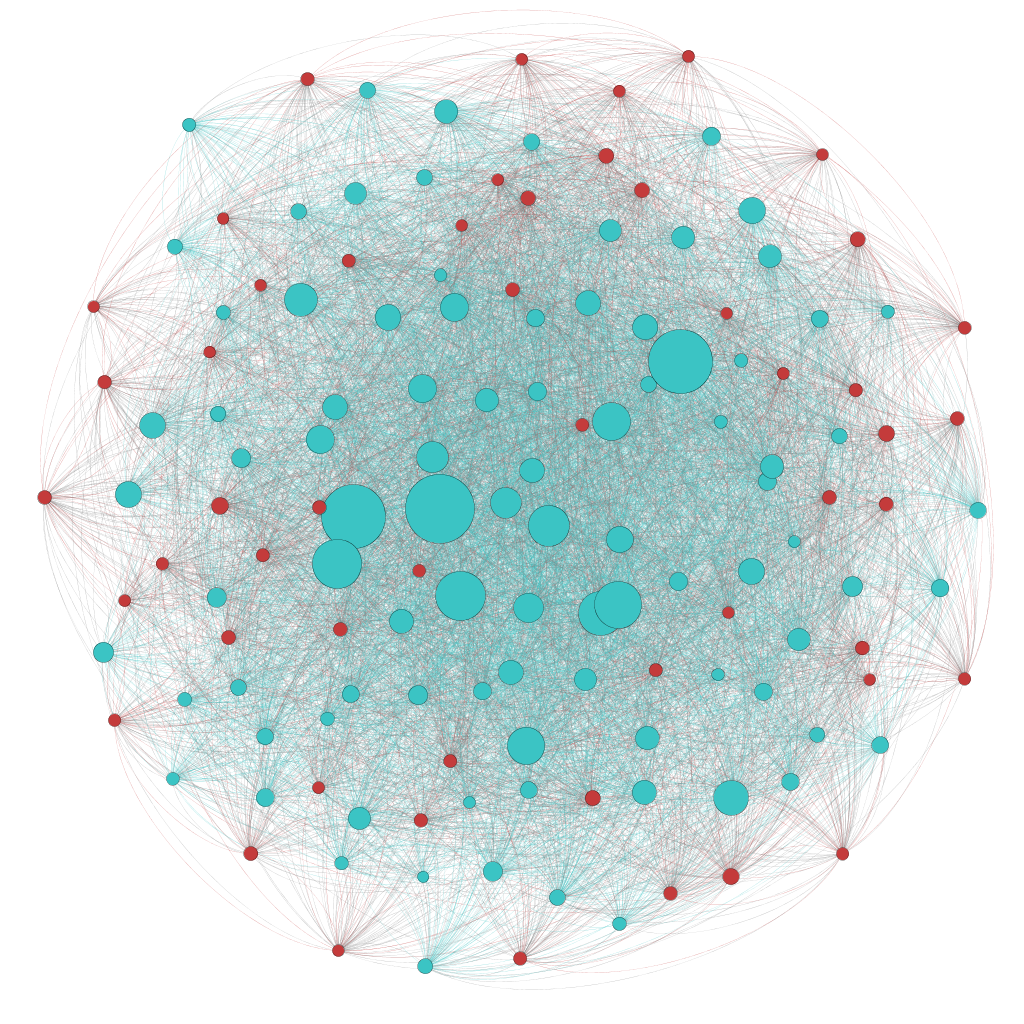
Gráfunk átmérője kettő, ami megfelel Ferreri i Cancho és Solé eredményeinek. A klaszterezési együttható azonban lényegesen magasabb, 0.75, mint az általuk mért 0.69 és 0.48. Ennek oka, hogy mi erősen szerkesztett, tudományos(abb) szövegeket használtunk, még az eredeti cikk a British National Corpus-ra támaszkodott. A teljes gráf valahogy így néz ki:
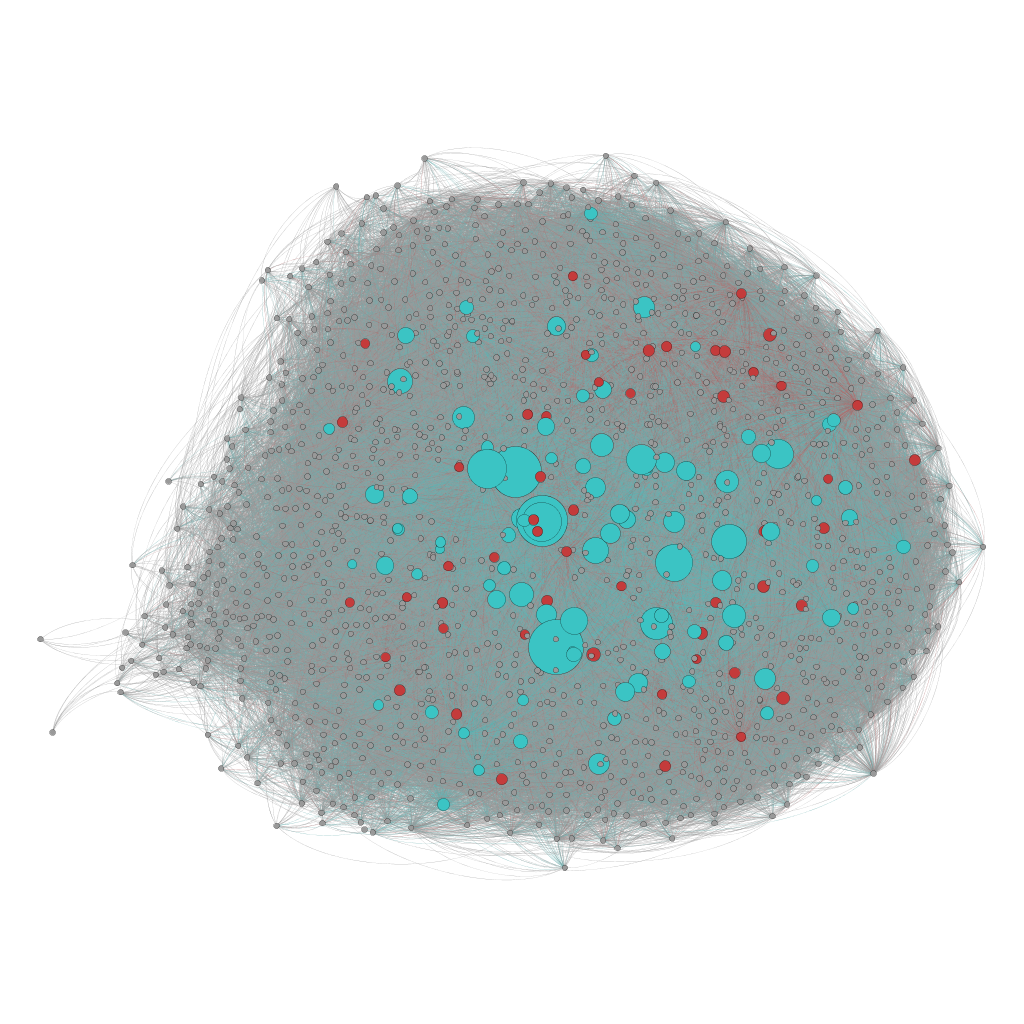
Ezen a gráfon már szürke csomópontok is vannak, ezek a Zipf-görbe hosszú farkán tanyázó szavak, melyek gyakorisága alacsony, elemben sok van belőlük. Reméljük látható, hogy ezek egy-egy piros, tehát közepes gyakoriságú szó körül "csomósodnak", ez lenne a kisvilágok egyik fő jellemzője.
Fokszámra (237 vagy nagyobb) szűrtünk az alábbi ábra elkészítéséhez, hogy csak központi elemeit mutathassuk meg gráfunknak.
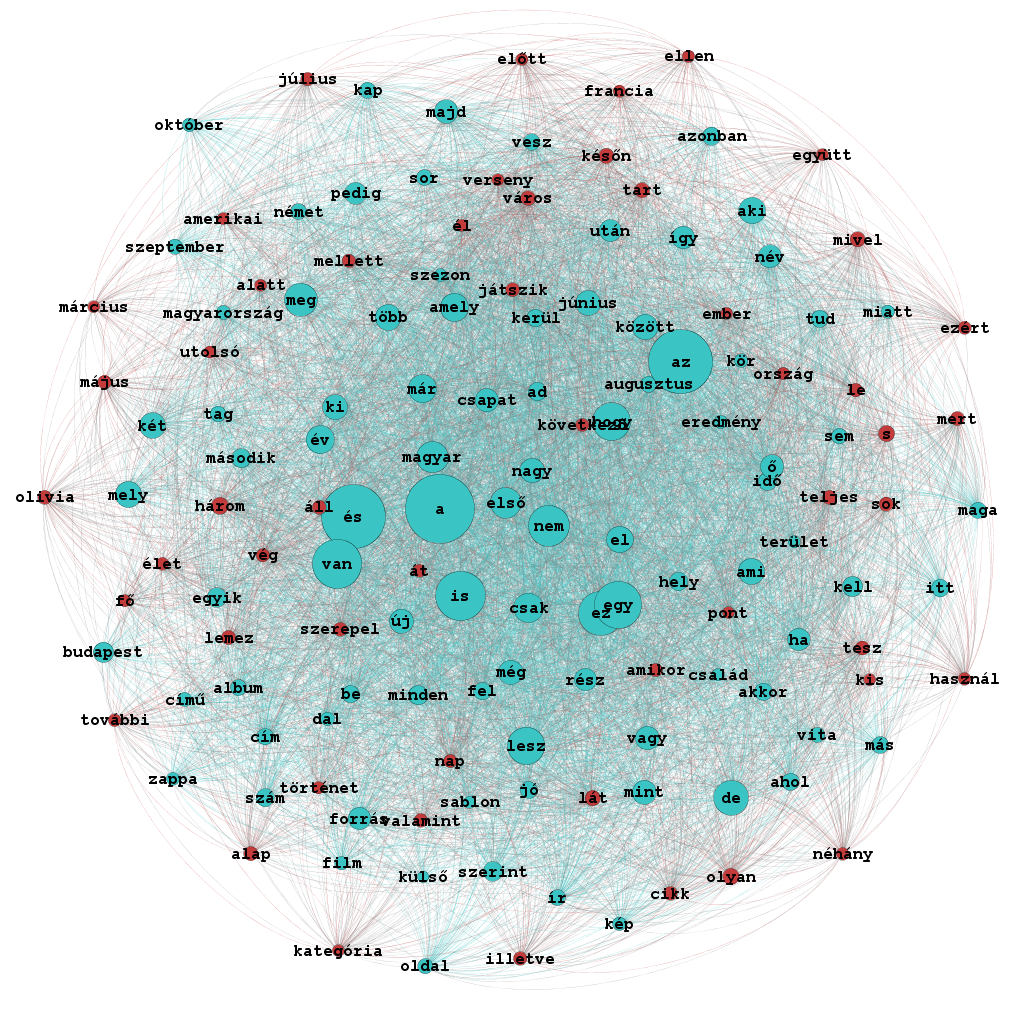
Az eredeti tanulmányban ezt nevezik „core kernel”-nek, azaz központi magnak. Mi is azt tapasztaljuk, hogy a funkciószavak (itt kékkel jelölve látható többségük, nagyságuk pedig fokszámuk függvénye) alkotta rész felel a többi szóval való összeköttetésért. Aki nagyon sasol, az észreveheti, hogy a piros-kék felosztás nem fedi teljesen a funkció- és tartalomszavak felosztást, de semmi sem lehet tökéletes.
Spekuláció
Ferrer i Cancho és Solé rámutattak arra, hogy a funkciószavak nem csak összekötik az egyes szavakat, hanem tulajdonképpen a különféle szótári osztályok között ezek létesítenek kapcsolatokat. A lexikon bővülése nem esetleges, hanem a kisvilágokra jellemzően egy-egy elem köré csoportosulva történik, ezért "fürtösödik" a hálózat, ez párhuzamba állítható a nyelvelsajátítással. Amennyiben a grammatikai funkciókat ellátó funkciószavak hálózata és a tartalommal rendelkező szavak lexikonja önálló rendszerek, melyek valahogy össze lettek huzalozva, érthető hogy milyen drasztikus következményekkel járhat valamelyik alrendszer sérülése, kiesése. Habár a kisvilágok (különösen a skálafüggetlen hálózatok, mint pl. az internet) a véletlen támadásokat viszonylag jól tolerálják, a célzott, központi elemeket kiiktató hibák súlyos következményekkel járhatnak rájuk nézve. Sajnos a tanulmány nagyon érintőlegesen foglalkozik csak ezzel a kérdéssel, de a felvetés nagyon érdekes.