Alig pár hónapja ment át egy program a Turing-teszten, a mesterséges intelligencia kutatói már azon agyalnak, miként lehetne életszerűbbé tenni ezen teszteket. Habár a Turing-teszten jól szereplő programok (mint látni fogjuk) "tudása" nem éppen hatalmas, valahogy intuitíven jónak érezzük Turing alapötletét; egy intelligens ágens képes társalogni, kérdésekre válaszolni csak úgy mint a Jeopardy-t 2011-ben megnyerő Watson.
Kacsák és tesztek
Turing tesztjének több változata van, az alap helyzet háromszereplős imitációs játék. Ebben egy kérdező egy géppel és egy emberrel beszélget s a társalgás végén meg kell mondania melyik partnere humán. A gép akkor nyer, ha rá esik a kérdező választása.
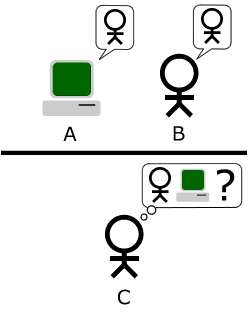
A bonyolultabb verzió szerint több kérdező vesz részt a játékban és akkor tekinthető intelligensnek a gép, ha a vizsgálatot végző személyek jelentős hányadát győzi meg arról, hogy "ő" ember.
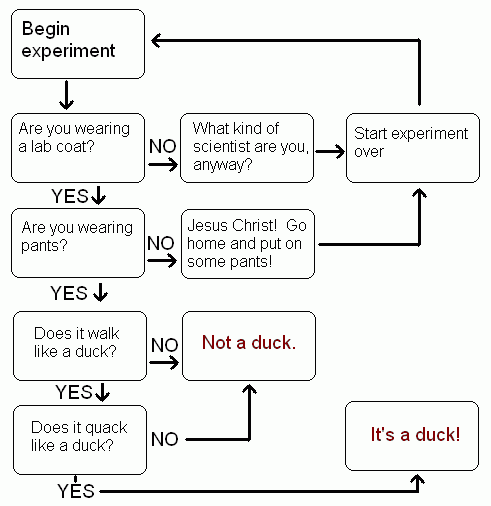
A Turing-teszt tkp. egy ún. duck test, hiszen annyit mond; ami úgy viselkedik mint egy ember, az intelligens és fordítva, ami intelligens, az úgy viselkedik mint egy ember.
Dennett szerint teljesen racionális, ha vélekedéseket, vágyakat, stb. tulajdonítunk valaminek, ami kellően komplex módon viselkedik. Ez nem jelenti azt, hogy ténylegesen intencionális, értelmes rendszerrel állunk szemben ilyenkor. Searle Az eleme, az agy és a programok világa című esszéjében a mesterséges intelligencia erős programjának nevezi azt az elképzelést, mely szerint egy megfelelően programozott számítógépre tekinthetünk úgy, mint egy elmére. Ez azzal jár, hogy elfogadjuk az agy és az elme kettősségét, hiszen a programok függetlenek az őket futtató gépektől. Searle szerint azonban az ilyen elme nem rendelkezhet intencionalitással, hiszen szimplán szimbólumokat manipulál. Hiába tűnik úgy, hogy intencionális a rendszer, ez csak a programozóinak köszönhető. Erről szól az előző posztunkban ismertetett kínai szoba gondolatkísérlet. De miről is szól Turing tesztje? Mit tesztel és miért? Hogyan lehet átmenni ezen a teszten, anélkül, hogy az intelligencia legkisebb jelét is mutassuk?
Mond gyorsan hogy Entscheidungsproblem!

Mindenki tudja, hogy Turingnak volt egy képzeletbeli gépe, a Turing-gép. Azután lett több nagyon konkrét gépe, melyekkel sikeresen törték fel Bletchley Parkban a német Enigma kódokat. Azt már kevesebben tudják, hogy Turing gépe a 19. század végén kezdődő matematikai és logikai válság lezárásának csodálatos pontja. A matematika megalapozásának programja a 19. században kezdődött, ennek terméke Frege munkássága, ami megalapozta a modern logikát (s egyben a számítástudományt). Sajnos Frege teljesen lemaradt arról, hogy learathassa a babérokat, mivel nagy összegző művében, Az aritmetika alaptörvényeiben Russel ellentmondást fedezett fel (Russel erről szóló levelét mellékletként leközölte Frege!) Innét elindult a hajsza a matematika megalapozása után. 1928-ban Hilbert fogalmazta meg, milyen követelményeket kell kielégítenie a szilárd alapoknak, ez a híres Entscheidungsproblem, vagy eldöntésprobléma. Ez tkp. azt követeli meg, hogy egy rendes algoritmusunk legyen, ami minden jólformált kijelentésre képes megadni hogy helyes-e, vagy másképp fogalmazva, levezethető-e rendszerünk axiómáiból. Gödel tétlei (mert kettő van neki) bebizonyították egy konzisztens rendszerben vannak igaz, de nem bizonyítható állítások s az ilyen rendszerek konzisztenciája nem bizonyítható a rendszeren belül. Gödel eredményei alig három évvel Hilbert problémájának ismertetése után jelentek meg. Turing egy kicsit tovább várt, mivel őt az izgatta, hogy mi "kiszámítható", azaz mit lehet levezetni, már ha érdeklődésünket a levezethető, bizonyítható állításokra korlátozzuk. Ez tulajdonképpen a matematikai tevékenység formalizálása, ami a híres Church-Turing tézishez vezetett. A Turing-gép nem más, mint annak formalizált leírása, hogy mit lehet bizonyítani, ezért lett az ezt bemutató tanulmány címe On Computable Numbers, with an Application to the Entscheidungsproblem. A Breaking the Code-ban a zseniális Derek Jacobi pár szóban így foglalja össze, mit is jelentett ez a kis dolgozat.
Gondolkodás, nyelv, más elmék
Turing, Church és Gödel tételei lényegében visszacsempészik a pszichologizmust a logikába. No nem abban az értelemben, hogy a modus ponens aktuális pszichikai állapotunk függvényében fog működni, hanem visszatért vele az intuíció. Wittgenstein előadásaira járva Turing elgondolkodhatott azon, hogy miért is kell formalizálni és stabilnak tudni a matematikai alapjait.
Wittgenstein:... Think of the case of the Liar. It is very queer in a way that this should have puzzled anyone — much more extraordinary than you might think... Because the thing works like this: if a man says 'I am lying' we say that it follows that he is not lying, from which it follows that he is lying and so on. Well, so what? You can go on like that until you are black in the face. Why not? It doesn't matter. ...it is just a useless language-game, and why should anyone be excited?
Turing: What puzzles one is that one usually uses a contradiction as a criterion for having done something wrong. But in this case one cannot find anything done wrong.
W: Yes — and more: nothing has been done wrong, ... where will the harm come?
T: The real harm will not come in unless there is an application, in which a bridge may fall down or something of that sort.
W: ... The question is: Why are people afraid of contradictions? It is easy to understand why they should be afraid of contradictions, etc., outside mathematics. The question is: Why should they be afraid of contradictions inside mathematics? Turing says, 'Because something may go wrong with the application.' But nothing need go wrong. And if something does go wrong — if the bridge breaks down — then your mistake was of the kind of using a wrong natural law. ...C. Diamond (ed.) Wittgenstein's Lectures on the Foundations of Mathematics
A fenti párbeszéd analógiája mondhatjuk, hogy akkor az ellentmondásmentesség egyben azt is jelenti, hogy működőképes is valami? Lehet olyan, hogy ellentmondásos, vagy eldönthetetlen és ennek ellenére működik valami? Elvileg igen, hiszen erről szólna (az eredeti kontextusától persze elszakítva) a Gödel-tétel. Ez lenne az intuíció, olyan igazságok megtalálása, melyek nem levezethetőek.

Az intuíció itt nem valami misztikus dolog, hanem valami, ami a Turing-gép keretein kívül van. De honnét tudjuk akkor, hogy valami többre képes mint egy Turing-gép? Hogyan állíthatjuk valakiről, hogy hozzánk hasonló intuícióval rendelkezik? Ezt nevezik a filozófusok a más elmék (other minds) problémájának. Wittgenstein privát nyelv argumentuma szerint ahhoz hogy feltételezzünk más elméket, szükség van a nyelvre.
"Mi lenne, ha az emberek nem nyilvánítanák meg fájdalmaikat (nem nyögnének, nem fintorítanák el az arcukat stb.)? Akkor egy gyereknek nem lehetne a 'fogfájás' szó használatát megtanítani." - Nos, tegyük fel, hogy a gyermek egy zseni, és maga talál ki egy szót arra, amit érez! - Ekkor persze ezzel a szóval nem tudná megértetni magát. - Szóval ő érti a nevet, de senkinek nem tudja jelentését megmagyarázni? - De mit is jelent, hogy 'megnevezte a fájdalmát'? - Hogy csinálta, hogy megnevezte a fájdalmat? ! És, akármit is tett - mi vele a célja? - Amikor azt mondják: "Nevet adott annak, amit érzett", akkor elfelejtik, hogy a nyelvben már sok mindennek készen kell állnia ahhoz, hogy a puszta megnevezésnek értelme legyen. És ha arról beszélünk, hogy valaki a fájdalomnak nevet ad, akkor itt a "fájdalom" szó grammatikája az, ami elő van készítve; jelzi azt a posztot, ahová majd az új szó kerül.
Wittgenstein: Filozófiai vizsgálódások
Habár lehetséges, hogy valaminek nyelvi megnyilvánulások nélkül intelligenciát tulajdonítsunk, az intencionalitás, miképp a Wittgenstein idézet rávilágít, társas és nyelvi természetű.
ELIZA, a legjobb beszélgetőpartner
Joseph Weizenbaum ELIZA programja a Turing-tesztre készülő programok őse. Az ELIZA-t leíró klasszikus tanulmányából vett példa szerint kb. így néz ki egy beszélgetés vele (a nagybetűs mondatok a géptől származnak).
Men are all alike.
IN WHAT WAY?
They're always bugging us about something or other.
CAN YOU THINK OF A SPECIFIC EXAMPLE?
Well, my boyfriend made me come here.
YOUR BOYFRIEND MADE YOU COME HERE
He says I'm depressed much of the time.
I AM SORRY TO HEAR YOU ARE DEPRESSED
It's true. I am unhappy
DO YOU THINK COMING HERE WILL HELP YOU NOT TO BE UNHAPPY
I need some help, that much seems certain.
WHAT WOULD IT MEAN TO YOU IF YOU GOT SOME HELP
Perhaps I could learn to get along with my mother.
TELL ME MORE ABOUT YOUR FAMILY
My mother takes care of me.
WHO ELSE IN YOUR FAMILY TAKES CARE OF YOU
My father.
YOUR FATHER
You are like my father in some ways.
WHAT RESEMBLANCE DO YOU SEE
You are not very aggressive but I think you don't want me to notice that.
WHAT MAKES YOU THINK I AM NOT VERY AGGRESSIVE
You don't argue with me.
WHY DO YOU THINK I DON'T ARGUE WITH YOU
You are afraid of me.
DOES IT PLEASE YOU TO BELIEVE I AM AFRAID OF YOU
My father is afraid of everybody.
WHAT ELSE COMES TO YOUR MIND WHEN YOU THINK OF YOUR FATHER
Bullies.
DOES THAT HAVE ANYTHING TO DO WITH THE FACT THAT YOUR BOYFRIEND MADE YOU COME HERE
Persze egy idő után fárasztó tud lenni ELIZA és könnyen ki lehet ejteni a szerepéből, de nagyon sokáig el lehet vele játszani. "Tudása" és fantasztikus "együttérzése" ún mintaillesztő szabályoknak köszönhető, melyek az ún. rogeriánus pszichológia visszakérdező módszerét imitálják. Norvig Paradigms of Artificial Intelligence Programming c. könyvében egy ELIZA típusú programhoz a következő szabályokat adja meg.
Minden (((?* ?x) W (?* ?y)) egy helyettesítő szabályt ad meg, pl. a (((?* ?x) computer (?* ?y)) akkor lép életbe, ha a bemenet tartalmazza a 'computer' szót, ami aktiválja a
válaszok valamelyikét (pl. véletlenszerűen választva). Sokkal inkább tűnik ez trükknek, mint valódi intelligenciának!
Az ELIZA effect nevet kapta ezért az a jelenség, amikor gépeket emberi tulajdonsággal ruházunk fel pusztán viselkedésük alapján. Maga Weizenbaum is erre a jelenségre akarta felhívni a figyelmet programjával, ahogy tanulmányának bevezetőjében írja:
It is said that to explain is to explain away. This maxim is nowhere so well fulfilled as in the area of computer programming, especially in what is called heuristic programming and artificial intelligence. For in those realms machines are made to behave in wondrous ways, often sufficient to dazzle even the most experienced observer. But once a particular program is unmasked, once its inner workings are explained in language sufficiently plain to induice understanding, its magic crumbles away; it stands revealed as a mere collection of procedures, each quite comprehensible. The observer says to himself "I could have written that". With that thought he moves the program in question from the shelf marked "intelligent" to that reserved for curios, fit to be discussed only with people less enlightened that he. The object of this paper is to cause just such a reevaluation of the program about to be "explained". Few programs ever needed it more.
Annyi bizonyos, hogy a Turing a tesztet az intelligencia szükséges és elégséges feltételeinek tekintette, azaz ha valami intelligens, akkor átmegy a teszten, ha nem, akkor megbukik. Úgy tűnik, bővítenünk kell a feltételek körét!