Nem kell sokat aludni következő meetupunkig! Május 28-án 18:00-tól várjuk az érdeklődőket a budai Colabs-ben! Meg tudhatjuk mit mond a kognitív nyelvészet az internetes trollokról, hogyan segítenek a Jobmonitor keresési adatai a munkanélküliség előrejelzésében és milyen a digitális testbeszéd. A rendezvény továbbra is ingyenes, de kérünk mindenkit, jelezze részvételi szándékát az esemény oldalán. 

Az alábbi előadásokkal várunk mindenkit:

• Petykó Márton (MTA NYI): Milyenek a trollok? (bővebben l. Márton Az internetes troll mint identitás kialakítása politikai blogok diskurzusaiban c. tanulmányát)
• Balogh Kitti (Precognox): A munkanélküliség előrejelzése a jobmonitor keresési adataival (bővebben l. korábbi Kereső Világ írásunkat)
• Clementine Consulting: A digitális testbeszéd (bővebben a Clementine oldalán)

Júniusban ismét NLP matinét tartunk! Két évvel ezelőtt volt ilyen, ideje hát megismételni! Várjuk cégek, intézmények, kutatóhelyek és érdekes projektek jelentkezését a zoltan.varju(kukac)precognox.com e-mail címre! Az időpont június 25. A rendezvény továbbra is ingyenes, de arra kérünk mindenkit, regisztráljon az esemény oldalán.

Szeretnénk alkalmat biztosítani arra, hogy a hazai kutatóhelyek, oktatási intézmények és az ipar szereplői kötetlen formában megismerhessék egymást. De ha akad egy érdekes projekted, azt is nyugodtan bemutathatod. Mindenki szigorúan öt percet kap arra, hogy elmondja mivel foglalkozik, milyen együttműködési lehetőségek érdeklik, keres-e új munkatársakat stb. Ez az az esemény, ahová nyugodtan hozhattok magatokkal egy raklapnyi marketing anyagot, névjegyet stb.!!!!! 

Életünk egyre több területén döntenek a gépek. Algoritmusok, gépi tanulási módszerek hoznak gyors döntéseket, melyek kihatnak életünkre. Kapunk-e hitelt, mennyi biztosítási díjat fizetünk, van-e kóros elváltozás egy szövetmintában, milyen filmeket ajánl nekünk kedvenc on-demand szolgáltatónk? Lassan megemésztjük, hogy a statisztikai módszer nem jár százszázalékos eredménnyel, de legalább amit csinál egy gép, azt csinálja akkor jól és konzisztensen. A gépek hatással vannak ránk, jó lenne tudni bízhatunk-e bennük...

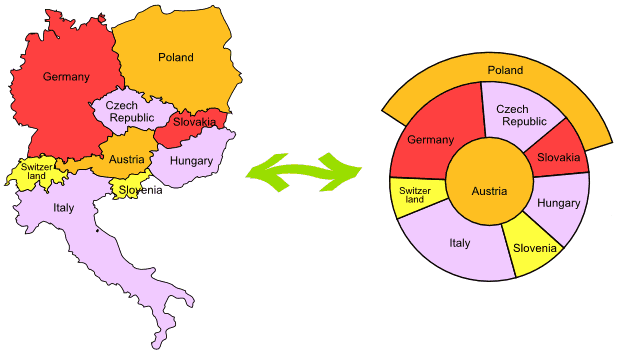
Az ún. négyszín-tétel a Wikipedia szerint "azt állítja, hogy egy tetszőleges régiókra osztott síkot, akár egy politikai térképet egy ország megyéiről, ki lehet úgy színezni legfeljebb négy szín felhasználásával, hogy ne legyen két azonos színű szomszédos régió." Amennyire egyszerűnek tűnik a kérdés, annyira nehéz volt bizonyítani! Appel és Haken bizonyítása alaposan felkavarta az elméleti matematika világát, mivel számítógépek végezték a munka jelentős részét. Sőt a bizonyítás korrektségének ellenőrzéséhez is számítógép szükségeltetik, amiért a matematika filozófiájával foglalkozók közül sokan nem is tekintik igazán bizonyítottnak a tételt, mások szerint ezzel a lépéssel a matematika elmozdult a természettudományok irányába (l. bővebben Tymoczko remek tanulmányát). A lényeg, hogy a bizonyítás majdnem 1500 konfigurációt vizsgál meg, hogy induktív módon "megmutassa" minden esetben elegendő a négy szín a térkép színezéséhez.

A gépi tanulás során általában az adatok alapján az algoritmus létrehoz egy absztrakciót, mely segítségével generalizálhat más, még nem látott esetekre. Ahogyan a négyszín-tétel bizonyítása sem fogható fel emberi ésszel, a gépi tanulás lépései is követhetetlenek egy ember számára. Egyik esetben sem arról van szó, hogy nem érthetőek! Formálisan definiált lépésekről van szó, a dolog "logikáját" értjük, csak nem tudjuk mi magunk elvégezni a szükséges lépéseket (különösen nem nagy számban, egymás után, gyorsan). Ahhoz, hogy meggyőződjünk arról, hogy ezen algoritmusok jól működnek, egyrészt formális bizonyítások szükségeltetnek (általában gépi úton végzik ezt is) illetve alaposan tesztelni kell a rendszereket.

A tesztelés tkp. a tudományos módszer alkalmazása a fejlesztésben. Karl Popper tette népszerűvé a falszifikáció fogalmát, ami annyit tesz, hogy egy rendes elmélet megadja cáfolhatóságának kritériumait. Egy rendes fejlesztés során nem csak arra ügyelnek, hogy mit kell tudnia egy szoftvernek, meg kell próbálni megcáfolni a működését is. A gépekben is csak annyira bízhatunk, mint a tudományban! Azonban manapság a tudománynál nincs jobban működő, transzparens, saját hibáinak kijavítását szem előtt tartó dolog a világon! A gépek hibázni fognak, kételkedni kell bennünk, ellenben tanulnak hibáikból és fejlődnek!

... csak beszéljenek rólad. Hihetetlennek hangzik, de talán van benne valami. A több csirip, több szavazat elv sokakat megdöbbentett és próbáltak magyarázatot találni arra, hogy amikor működik, akkor miért is működik. Az eddigi legjobb ötlet a pollyanna hipotézis volt, miszerint a pozitív érzelmi töltetű szavak gyakorisága magasabb, ezért a magasabb említésgyakorisággal együtt kell, hogy járjon a pozitív polaritás is. A Neticle a választások előtt vizsgálta a magyar webet és meglepő eredményre jutott: a több csirip elv nagyon jól működik, de nincs mögötte a pollyanna jelenség!

Ahogy a fenti ábrán is látható, az említésgyakoriság sokkal jobban közelíti a tényleges választási eredményeket. Persze a pozitív említések aránya se kutya, de nézzük a következő ábrát!

Ez az ábra a közvéleménykutatók és a Neticle említésgyakoriságon ill. pozitív említéseken alapuló eredményeinek a tényleges választási arányoktól való eltérését mutatja. Látható, hogy a puszta említésgyakoriság közelíti a legjobban  a valós számokat, a pozitív említések ellenben rosszul muzsikáltak!

Látható, maga a more tweets, more votes elv a magyar adatok tükrében megerősítést nyert. Az is igaz, hogy a legmagasabb említést elérő polaritása a leginkább pozitívabb, ellenben a szentiment megoszlása eltér az említésekétől (l. a Kormányváltás és a Jobbik adatait!). A legkézenfekvőbb magyarázat az ún. puszta kitettség (mere exposure) effektus lehet, azaz a magasabb említésgyakoriság ismertebbé, s ezáltal pozitívabbá teszi a szereplőket, de csak bizonyos említésszám felett. Persze ez csak spekuláció a részünkről, kommentben nyugodtan lehet tippeket adni a jelenség magyarázatára!

(Köszönjük Szekeres Péternek, a Neticle vezető kutatójának az ábrákat!)

Emily M. Bender könyvét bemutató posztunk kapcsán sokan panaszkodtak, hogy a kötet nem éppen könnyen hozzáférhető az átlag magyar közönség számára. Nem kell elkeseredni, van olyan magyar könyv is a piacon, ami minden jobb könyvtárban megtalálható és még a nyelvészet alapjait is megismerheti belőle a kedves olvasó! Szilágyi N. Sándor Világunk, a nyelv c. könyvét ajánljuk Bender könyve helyett/mellett mindenkinek!

A kötet józan paraszti észnél nem igényel többet. Alapvetően nem tesz mást, mint szépen végigvezeti az olvasót a hagyományos nyelvészeti témákon (de nem a bevett sorrendben, a hangtantól a jelentéstanig, hanem egy kicsit kalandozva). Nem törekszik olyan formalizmusra, mint Bender, de ez inkább előnye, mint hátránya. Mivel rövid és olvasmányos, hamar el is lehet olvasni és ha mást nem, annyit mindenképpen tanul az ember belőle, hogy a nyelv csodálatos dolog és bizony nem egyszerű megfejteni. Ezzel nem árt tisztában lenni a nyelvtechnológiában is! A szemlélet sokat segíthet a további szakirodalom befogadásában és a felmerülő problémák értelmezése során is - ami pár óra olvasgatást igazán megér. Hajrá!