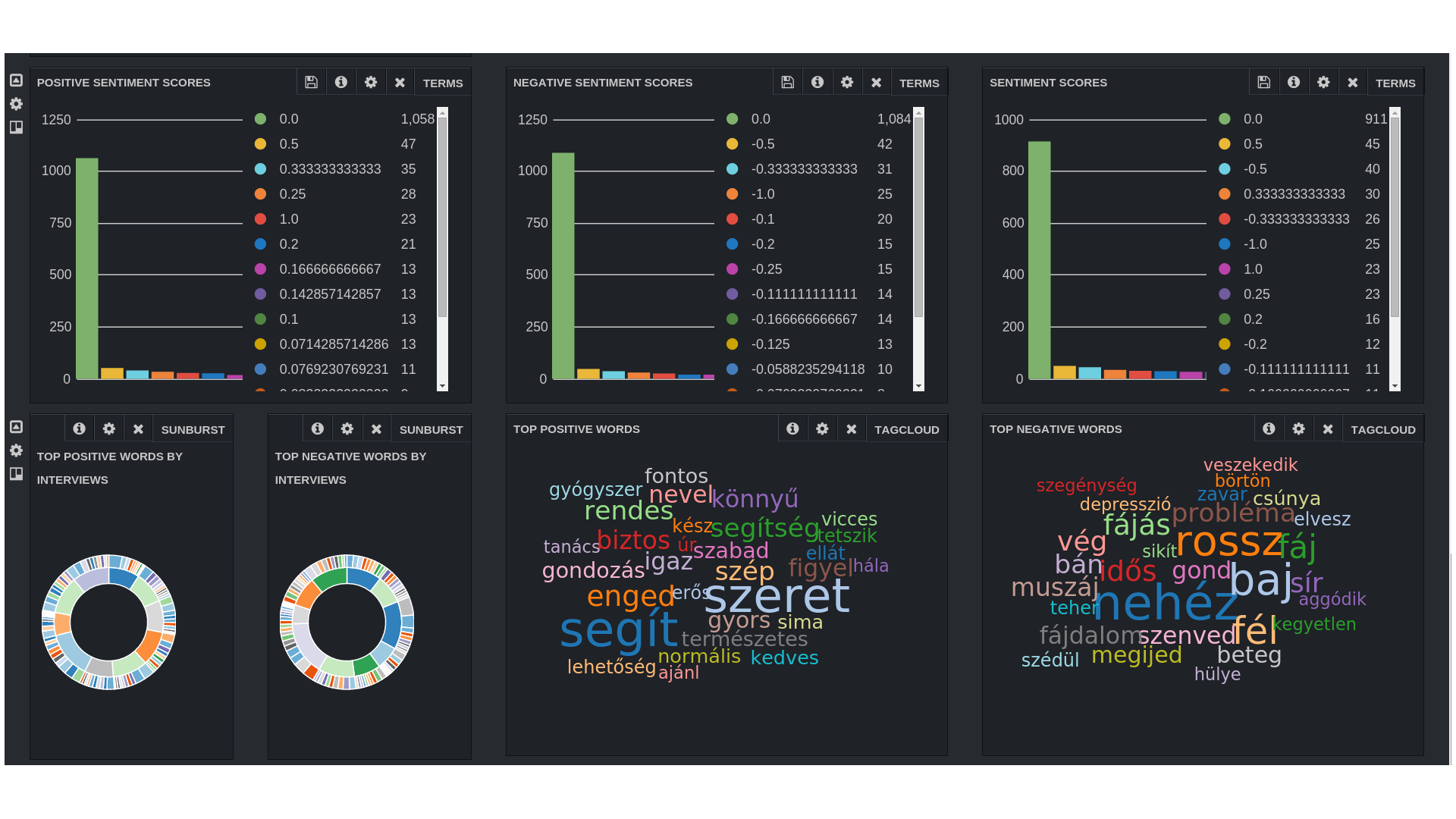
Miről lehet fogalmunk? Hogyan tudunk határt húzni fogalmaink közé? Hogyan lehetséges az, hogy a go is egy játék, meg a foci is az? Mi vetítjük a világra fogalmainkat, vagy azokat a dolgok valamilyen természetes tulajdonsága alapján alkotjuk meg? A tudományos fogalmak helyesebbek-e, mint a “hagyományos” fogalmaink? Egyáltalán, miért szeretünk mindent kategorizálni?
A klaszterezés illúziója
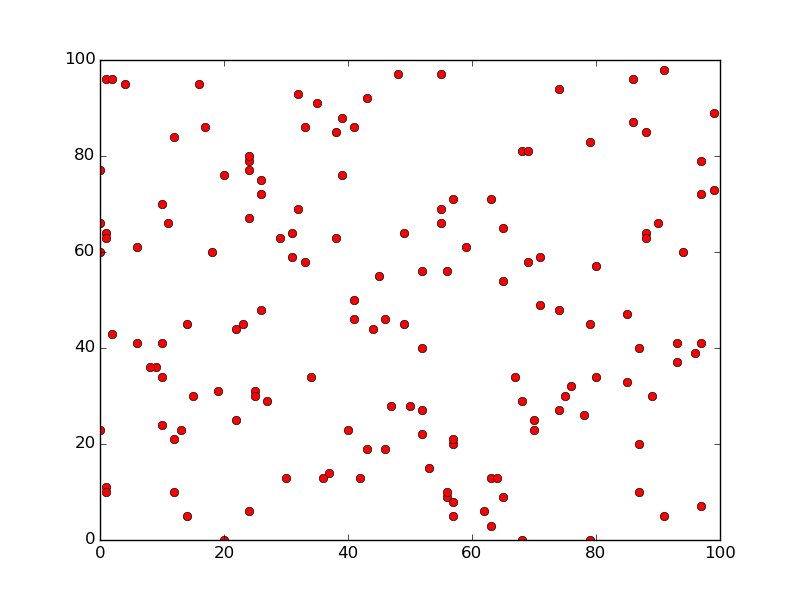
Nézze meg az alábbi ábrát alaposan. Észrevesz valamilyen szerveződést a pontok között?
És ha így mutatjuk?
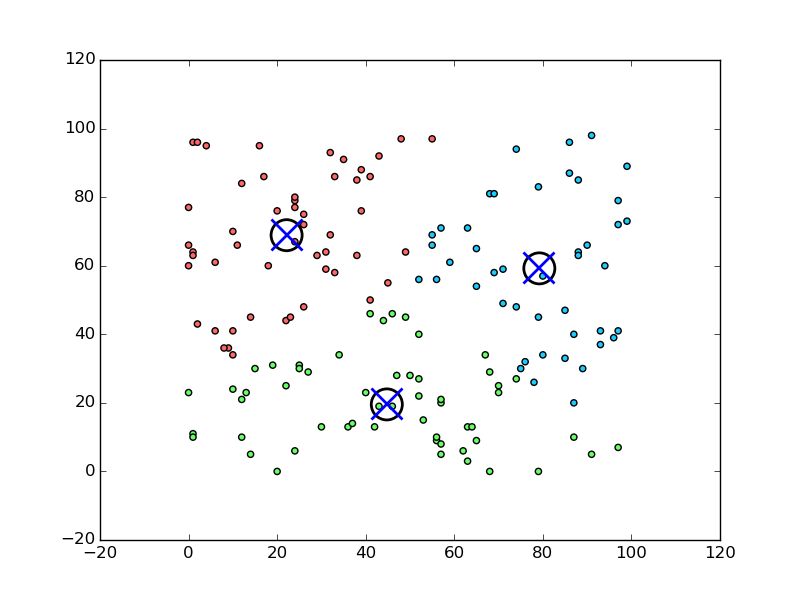
Nyilvánvaló? Van benne valami? Hülyeség? Igen, ha arra gondolt hogy ez hülyeség, akkor jól gondolta. Az első ábrát úgy készítettük, hogy 150, random generált pontot tettünk rá. Ezután egy nagyon kedvelt klaszterezési eljárással kerestünk hasonlóságot a pontok között, és hát találtunk is, ezt mutatja a második ábra. Lehet szidni az algoritmust (jelen esetben ez a k-means), hogy miért talál ott is rendszert, ahol nincs, de az emberek is így működnek.
Az emberek szeretnek belelátni csoportokat, vagy tudományoskodósabban klasztereket, a random mintákba. Ezt nevezzük Tversky és Kahneman nyomán a klaszterezés illúzójának, ami egy ún. kognitív torzulás és abból ered, hogy nem elég nagy mintát vettünk a random sokaságból. Ez azonban komoly problémákhoz vezethet, hiszen mintázatokat látunk ott, ahol nincsenek. A probléma másik vége az, hogy egyszerűen lehetetlen lenne elboldogulni a világban klaszterezés nélkül.
Prediktív elmék
Nem csak az gazdaságtalan, ha minden egyes dolognak külön nevet adunk, az is roppant pazarló, ha mindenre odafigyelünk. A kognitív tudományokban egyre elfogadottabb az ún. prediktív kódolás irányzata, mely szerint az elménk elvárja hogy a dolgok a megszokott mederben folyjanak és csak akkor kezd keményen dolgozni, ha elvárásainak ellentmondó dolgokat tapasztal. Ilyenkor a mintázattól való eltérésre figyeltünk fel és rögtön egy másik mintázat által suggalt cselekvési sort hajtottunk végre. Például, amikor nem találjuk a lakáskulcsot a megszokott helyén, akkor megtörik a rutinunk, de ha nem először fordult elő ez velünk, akkor rögtön módszeresen kezdünk utána kutakodni. A prediktív kódolás nagyon elmés magyarázat arra, hogy miért keresünk mindenhol mintázatokat, azonban arra nem ad választ, hogy miért találunk mintázatokat és mennyire hasznosak, netán “igaziak” azok a klaszterek, amiket a világ dolgaira húzunk.
Természetes fajták
A filozófia úgy fordítja le a fenti kérdést, hogy léteznek-e természetes fajták (natural kinds). A fogalmat Quine vezette be a mai analitikus filozófiába. Quine számára a természetes fajták olyan fogalmak, melyek segítségével induktív következtetéseket tudunk végezni. Ilyenek például a kémai elemek, hiszen tulajdonságaik alapján megjósolhatjuk mi történik velük ha melegítjük vagy éppen összekeverjük azokat. Ebből következik, hogy a természetes fajták a fizika törvényei által szabályozottak. De mi a helyzet az olyan hétköznapi fogalmakkal mint például a fekete vagy a holló? Ezek is alkalmasak az indukciós következtetésre, mivel a “minden holló fekete” hipotézis megalkotásához szükséges hogy legyenek fekete dolgok és legyenek hollók. A nem-fekete és nem-holló dolgok ellenben nem természetes fajták.
Persze olyat, hogy nem-fekete, vagy nem-holló, nem szoktunk mondani. Olyanokat szoktunk mondani, hogy emberek, állatok, székek, kutyák és ezekkel nagyon szépen működnek következtetési szabályaink, legyenek azok induktívak, vagy deduktívak. Gondolhatnánk, a nyelv nagyon remekül felvértezett minket arra, hogy elboldoguljunk a világban. Ellenben régebben teljesen természetesen vádoltak meg és ítéltek el embereket boszorkányság vádjával. Mondhatjuk, egy időben a borszorkányság természetes fajta volt, hiszen sok dolgot meg lehetett magyarázni, ha feltettük egy illetőről hogy boszorkány. Ma már úgy gondoljuk, a boszorkányság fogalma nem valós, nem használható, hiszen nincsenek olyan tulajdonságai az embereknek, melyek alapján joggal alkalmazható rájuk a szó. Valami hasonló történt a kémia történetében híres flogisztonelmélettel is. Sok tudós rákapott az égés magyarázatában a flogiszton feltételezésére, amit látni nem láthat senki, de ha feltesszük hogy minden éghető anyagban van valami közös, amitől az éghető, akkor eljutunk tudományos fogalomhoz. Így az égés, jobban mondva a tűz kikerült az ősi alapelemek közül és egy megmagyarázható természeti jelenséggé vált. A flogiszton létét tudományos kísérletekkel igyekeztek bizonyítani, amik amúgy Lavoisier ma is elfogadott magyarázatának megjelenéséig nagyon meggyőzőek voltak.
Quine elve működni látszik, a boszorkányság fogalma nem alkalmazható jól induktív következtetésekre, ahogy a flogiszton sem. Mondhatjuk, az empíria tükrében változhatnak fogalmaink. Az ún. elminatív materializmus elmefilozófiai irányzata szerint a “hagyományos” vagy szakszóval népipszichológia fogalmait a tudomány szépen lassan lebontja és rendes fizikai magyarázatra épülő fogalmakkal váltja fel. Ezzel csak annyi baj van, hogy a tudományos fogalmak is állandóan változnak, mindig jön egy “igazabb” elmélet, “jobb” fogalmakkal. A másik probléma az, hogy a legracionálisabb tudós sem akarja a vacsoráját annak összetevőinek képleteiben leírva megrendelni, szerelmének nem a benne lezajló kémiai és fiziológiai reakciókt fogja leírni, stb.
A tudomány nyelve is emberi nyelv
Az eliminatív materializmus legnagyobb hibája az, hogy ha mindent visszavezetünk a fizika vagy a matematika nyelvére, akkor is egy nagyon emberi nyelvet kapunk. Hiába a szép formalizmus, ha valaki fizikus, kémikus, orvos, vagy éppen irodalmár, filozófus, stb. akar lenni, akkor nem tudja a szakmát csupán könyvekből megtanulni. Hiába olvassa el valaki ezerszer, hogyan kell egy rendes kémiai kísérletet megcsniálni, ha nem mutatja meg neki valaki és vezeti végig az eljáráson, akkor nagyon könnyen baj lehet a dologból. Még a matematika sem mentes ezektől! Polányi Mihály, aki maga is gyakorló természettudós volt, tudományfilozófiai műveiben ezt nevezi hallgatólagos tudásnak.
Polányi az autóvezetés példáján keresztül szemlélteti a hallgatólagos tudás mibenlétét. Leírhatjuk a kormány tekerésének finom részleteit, a KRESZ szabályait, a járművezetés illemtanát, de az egyáltalán nem ugyanaz, mint amikor valaki ténylegesen vezet, érzi hogy mikor kell megnyomnia a fékpedált, elengednie egy besorolni akaró autót, vagy egy kicsit gyorsítani a sárgán villogó lámpánál. Az autóvezetéshez kapcsolódó fogalmakat nem önállóan, vagy egymáshoz viszonyítva tanuljuk meg leírások alapján, hanem használat közben. A tudomány is így működik és ez egyáltalán nem jelenti azt, hogy fogalmai zavarosak, vagy következetlenek lennének, csak az van hogy a tudományt is emberek művelik.
Mitől fogalom egy fogalom?
Láthattuk, a fogalmak, klaszterek, vagy mintázatok átszövik az emberi életet. De hogyan alakulnak ki? Mi köti össze az adott fogalom alá tartozó dolgokat?
“Vizsgáld meg például egyszer a azokat a folyamatokat, amelyeket “játékok”-nak nevezünk. A táblajátékokra, kártyajátékokra, labdajátékra, küzdősportokra stb. Gondolok. Mi a közös mindezekben? - Ne mondd, hogy “Kell valami közösnek lennie bennük, különben nem hívnák őket ‘játékok’-nak” - hanem nézd meg, van-e valami közös mindben. - Mert ha menézed őket, nem fogsz ugyan olyasmit látni, ami mindben közös, de látsz majd hasonlóságokat, rokonságokat, mégpedig egész halomnyit. Szóval ne gondolkozz, hanem nézz! [...] ezeket a hasonlóságokat nem tudom jobb szóval jellemezni, mint hogy “családi hasonlóság”-ok; mert így fedik át és keresztezik egymást azok a különböző hasonlóságok, amelyek egy család tagjai között állnak fenn: termet, arcvonások, a szem színe, a járás, a temperamentum stb., stb.” (Wittgenstein PHI §66-67)
Wittgenstein családi hasonlóság koncepciója a modern kognitív nyelvészet egyik origója. Az ún. prototípus-elmélet alapítója Eleanor Rosch a filozófiai alapokról indulva arra volt kíváncsi, hogy az egyes kategóriák elmeit mennyire tartják az emberek tipikus, vagy reprezentatívnak. Ezzel amolyan sorrendet állapíthatunk meg a kategória egyes elemei között. Ez már jó alap a fenti idézetben emlegetett hasonlóság definiálásához. Ennél tovább is léphetünk egy kicsit, vegyük például az ország fogalmát. Rangsoroljuk tipikusság szerint az országokat, majd nézzünk egy adatsort hogy hány négyzetkilométer a területük. Képzeletbeli adatsorunk első pár sora valahogy így nézne ki:
|
Ország
|
Tipikusság
|
Méret
|
Lakosság
|
|
Meseország
|
2
|
100
|
22
|
|
Csodaország
|
3
|
50
|
30
|
|
Seholország
|
3
|
60
|
50
|
|
Nagyország
|
1
|
55
|
40
|
|
Kisország
|
4
|
4
|
1
|
Adatainkat ábrázoljuk egy ploton, ahol az egyik tengely a tipikusság, a másik pedig a terület.
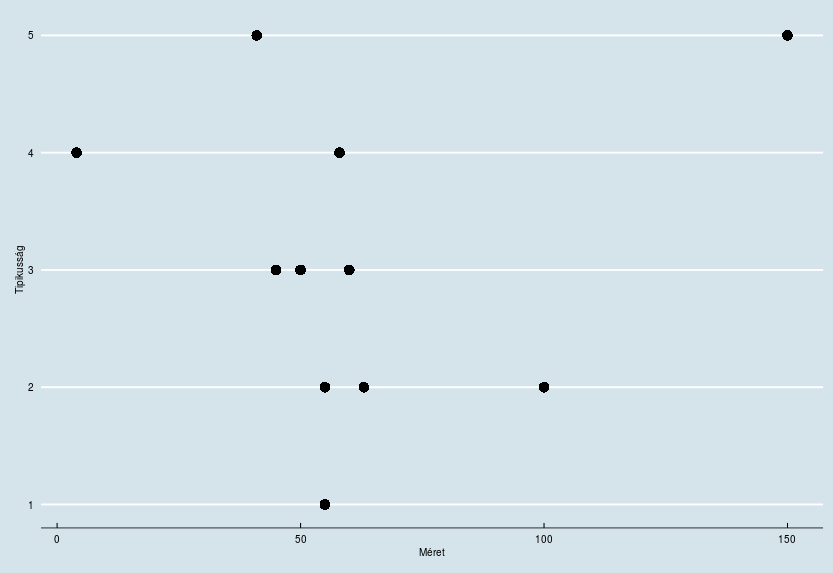
Láthatjuk, a tipikus országok méretük tekintetében sincsenek messze egymástól. Most nézzük meg, hogy a méret és a lakosságszáma szerint hogy néz ki a plotunk.
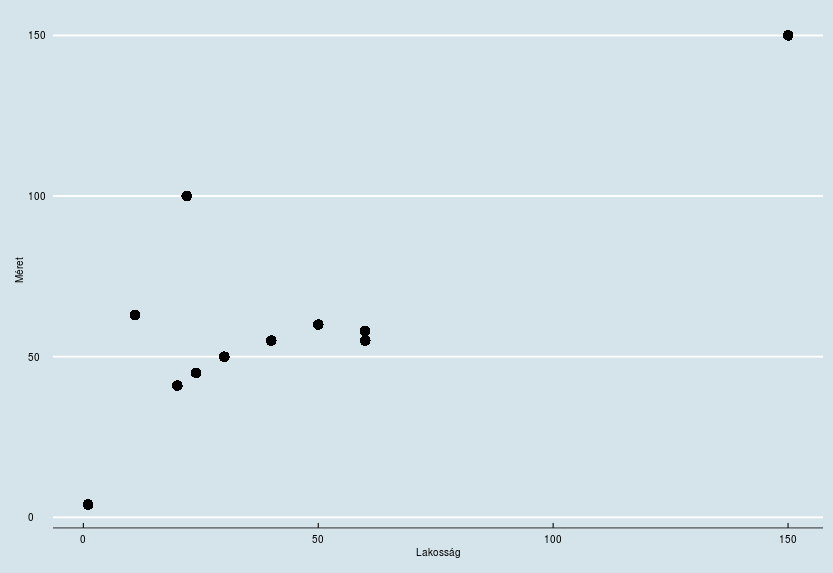
Itt is, az átlagos nagyságú és átlagos lakosságszámú országok összetartanak és példánkban ezek a legtipikusabb országok.
A fenti példában ún. metrikus térbe helyeztük az országokat két dimenzió mentén. De tovább is mehetünk és további jellemzőket is mérhetünk, ezek további dimenziókat jelentenek. Az egyes pontok között lemérhetjük a távolságot. Sőt, nem is kell tudnunk előre miről gyűjtünk adatokat, elég rögzíteni milyen értékeket társítunk egy-egy elemhez az adott dimenziók mentén. Ha klaszterezni szeretnénk az adatainkat, akkor nagyon jó stratégia, hogy szeretnénk egymáshoz közelállóakat találni és egyszerű geometriai számításokkal ezt el is érhetjük. Egy-egy csoport központi elemét, melytől a többi elem távolsága a legkisebb, tekinthetjük a csoport prototípusának. A legtöbb klaszterző algoritmus ezen eljárás változatait használja és igen jó eredményeket produkálnak általában. Az is nagyon meggyőző, hogy a tipikalitási ítéletek többnyire vissza szoktak tükröződni ezekben a klaszterezésekben. De sajnos nem minden esetben.
Túl a metrikus tereken
Nagyon korán, a hetvenes években bebizonyosodott Tversky úttörő munkáinak hála, hogy a metrikus terekre jellemző szép matematikai tulajdonságok nem jellemzőek az emberi gondolkodásra. Egy rendes metrikus térben A és B pont között a távolság pontosan akkora, mint B és A pontok között. Ellenben a hasnolósági ítéletekben ez nem igaz, pl. “Mennyire hasonlít Észak-Korea az Egyesült Államokra” és a “Mennyire hasonlít az Egyesült Államok Észak-Koreára?” kérdésekre nagyon eltérő válaszokat szoktak kapni a kutatók. Hasonlóan gyakran sérül az ún. háromszögelés elve, azaz az A és B közötti távolság, hozzáadva a B és C közötti távolsághoz, nagyobb vagy egyenlő A és C távolságánál (röviden ha két pot között egy harmadikat is érintek, akkor minimum ugyanannyit, vagy többet kell utaznom mint egyedül a két pont között). Például Szerbiát hasonlónak tekinthetjük Magyaroroszághoz (mint poszt-kommunista országok pl.), Magyarországot hasonlóbbnak Szlovákiához (pl. mert mindkettő EU-tag). Ebből elvileg következnie kell, hogy Szerbia Szlovákiához vagy kevésbbé, vagy Magyarországgal egyenlő mértékben hasonló (amit sokan megkérdőjeleznek intuitívan).
A rendes metrikus terektől való eltérésnek több oka lehet. Az egyik legfontosabb az, hogy fogalmaink nem rendesek, nem monothetikusak, azaz nem az összes dimenzió mentén vesznek fel értékeket. Ez még önmagában nem lenne baj, hiszen önmagában az egy jó tulajdonság is lehetne ami alapján szépen elkülönülhetnének. Gondoljunk bele Wittgenstein játék példájába. Milyen szép lenne ha a labadjátákok a csoportosan, labdával játszott játékok osztályát adnák ki, a kártyajátékok az egyedül, párban, többen játszottakét, stb. Nem csak a játék fogalma lenne szépen lefedve, hanem annak alkategóriái is. Erre akadnak olyan furcsaságok mint a freestyle foci, amit egyedül űznek, de labdával.
Van fogalmunk valamiről?
Annak ellenére tudunk nap mint nap fogalmakat használni, tanulni és alkotni, hogy nem sok fogalmunk van arról, mit jelent fogalmakkal rendelkezni. Nagyon jó lenne többet megtudni erről a területről, hiszen az alapvető kíváncsiságon túl gyakorlati haszna is lehetne eme tudásunknak. Az asszisztív technológiák a tanulási nehézségekkel küzőknek segíthetnének, a tudományos munkában és az üzleti életben pedig a különböző klaszterező és klasszifikációs algoritmusok már ma is létfontosságúak.